Question

1．已知函數f（x）=$\left\{\begin{array}{l}{2-2x，0≤x＜1}\\{lnx，1≤x≤e}\end{array}\right.$．
（1）求f（f（$\sqrt{e}$））；
（2）若x₀滿足f（f（x₀））=x₀，且f（x₀）≠x₀，則稱x₀為f（x）的二階不動點，求函數f（x）的二階不動點的個數．

Answer 1

分析 （1）利用分段函數，逐步求解函數值即可．
（2）利用分段函數求出f（f（x₀））的解析式，然后通過求解方程得到函數f（x）的二階不動點的個數．

解答 解：（1）∵f（x）=$\left\{\begin{array}{l}{2-2x，0≤x＜1}\\{lnx，1≤x≤e}\end{array}\right.$．
∴f（$\sqrt{e}$））=ln$\sqrt{e}$=$\frac{1}{2}$，
∴f（f（$\sqrt{e}$））=f（$\frac{1}{2}$）=2-2×$\frac{1}{2}$=1；
（2）函數f（x）=$\left\{\begin{array}{l}{2-2x，0≤x＜1}\\{lnx，1≤x≤e}\end{array}\right.$．x∈[0，$\frac{1}{2}$），f（x）=2-2x∈（1，2]，
x∈[$\frac{1}{2}$，1），f（x）=2-2x∈（0，1]，
x∈[1，e]，f（x）=lnx∈（0，1），
∴f（f（x））=$\left\{\begin{array}{l}{ln（2-2x），0≤x＜\frac{1}{2}}\\{2-2（2-2x），\frac{1}{2}≤x＜1}\\{2-2lnx，1≤x≤e}\end{array}\right.$，
若x₀滿足f（f（x₀））=x₀，且f（x₀）≠x₀，則稱x₀為f（x）的二階不動點，
所以：x₀∈[0，$\frac{1}{2}$），ln（2-2x₀）=x₀，由y=ln（2-x₀），y=x₀，圖象可知：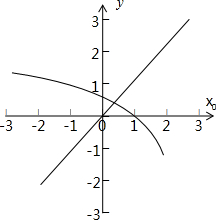

存在滿足題意的不動點．
x₀∈[$\frac{1}{2}$，1），-2+4x₀=x₀，解得x₀=$\frac{2}{3}$，滿足題意．
x₀∈[1，e]，2-2lnx₀=x₀，即2-x₀=2lnx₀，由y=2-x₀，y=2lnx₀，圖象可知：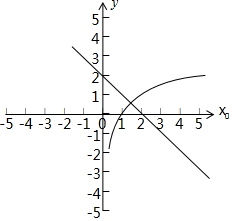

存在滿足題意的不動點．
函數f（x）的二階不動點的個數為：3個．

點評 本題考查新定義的應用，考查數形結合，分類討論思想以及轉化思想的應用，考查計算能力．