
分析 (1)利用定義法求數列{an}的通項公式.
(2)利用定義法求數列{bn}的通項公式,設F(n)=anbn+2=2-$\frac{1}{n+2}$-$\frac{1}{(n+2)^{2}}$,顯然,F(n)在n∈N*單調遞增.結合函數單調性求實數M的取值范圍.
解答 解:(1)∵2Sn=(n+1)an+n-1,①
∴2Sn-1=nan-1+n-2,②.
由①-②得:2an=(n+1)an+nan-1+1,③
∴2an+1=(n+2)an+(n+1)an+1+1,④
由④-③得:nan-1+nan+1=2nan即an-1+an+1=2an,
∴數列{an}是等差數列.
又∵2S2=3a1+1,a1=2,
∴a2=3,d=1,
∴an=n+1;
(2)∵$\frac{{a}_{1}}{\sqrt{{b}_{1}+1}}$+$\frac{{a}_{2}}{\sqrt{{b}_{2}+1}}$+…+$\frac{{a}_{n}}{\sqrt{{b}_{n}+1}}$=$\frac{{n}^{2}+n}{2}$(n∈N*),①
∴$\frac{{a}_{1}}{\sqrt{{b}_{1}+1}}$+$\frac{{a}_{2}}{\sqrt{{b}_{2}+1}}$+…+$\frac{{a}_{n-1}}{\sqrt{{b}_{n-1}+1}}$=$\frac{(n-1)^{2}+n-1}{2}$(n∈N*),②
由①-②得:$\frac{{a}_{n}}{\sqrt{{b}_{n}+1}}$=$\frac{{n}^{2}+n}{2}$-$\frac{(n-1)^{2}+n-1}{2}$=n⇒bn=$\frac{2n+1}{{n}^{2}}$(n∈N*).
即F(n)=anbn+2=$\frac{(n+1)(2n+5)}{(n+2)^{2}}$=$\frac{2{n}^{2}+7n+5}{(n+2)^{2}}$=$\frac{2(n+2)^{2}-(n+2)-1}{(n+2)^{2}}$=2-$\frac{1}{n+2}$-$\frac{1}{(n+2)^{2}}$,
顯然,F(n)在n∈N*單調遞增.
∴F(n)≥F(1)=$\frac{14}{9}$,
∴M≤$\frac{14}{9}$.
點評 本題目主要考查了利用數列的遞推公式求解數列的通項公式,解題中要注意等比數列的通差公式的應用.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源: 題型:選擇題
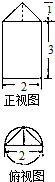 一個圓柱與一個三棱錐的組合體的正視圖和俯視圖如圖所示,則該幾何體的側視圖的面積為( )
一個圓柱與一個三棱錐的組合體的正視圖和俯視圖如圖所示,則該幾何體的側視圖的面積為( )| A. | 6 | B. | $\frac{13}{2}$ | C. | 7 | D. | 4π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{36}$ | D. | $\frac{25}{36}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第二象限角或第三象限的角 | B. | 第一象限角或第四象限的角 | ||
| C. | 第三象限角或第四象限的角 | D. | 終邊在直線y=-x左下方的角 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
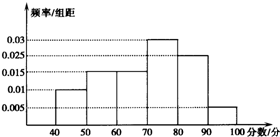 從參加環保知識競賽的學生中抽出60名,將其成績(均為整數)整理后畫出的頻率分布直方圖如圖所示,觀察圖形,回答下列問題:
從參加環保知識競賽的學生中抽出60名,將其成績(均為整數)整理后畫出的頻率分布直方圖如圖所示,觀察圖形,回答下列問題:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
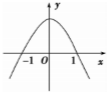 已知函數f(x)=ax3+bx2+cx在點x0處取得極小值-4,其導函數的圖象經過(-1,0),(1,0),如圖所示:
已知函數f(x)=ax3+bx2+cx在點x0處取得極小值-4,其導函數的圖象經過(-1,0),(1,0),如圖所示:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com