
分析 先求出命題p、q為真時m的范圍,由p、q一真一假列式求解
解答 解:命題p真:?c>0,y=(5-c)x在R上是增函數,∴0<c<4,
命題q真:?x∈R,x2+2x+c>0⇒△=4-4c<0⇒c>1;
若p∧q為假命題,p∨q為真命題,則p、q一真一假,
①p為真q為假時,$\left\{\begin{array}{l}{0<c<4}\\{c≤1}\end{array}\right.$⇒0<c≤1;
②p為假q為真時,$\left\{\begin{array}{l}{c≤0\\;或c≥4}\\{c>1}\end{array}\right.$⇒c≥4;
綜上實數c的取值范圍為:(0,1]∪[4,+∞)
點評 本題考查了命題真假的應用,屬于基礎題.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 最大值8 | B. | 最小值10 | C. | 最大值12 | D. | 最小值14 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({1,\sqrt{3}}]$ | B. | $({1,\sqrt{2}}]$ | C. | $[{\sqrt{3},+∞})$ | D. | $[{\sqrt{2},+∞})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若$\overrightarrow{a}$,$\overrightarrow{b}$滿足|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,且$\overrightarrow{a}$與$\overrightarrow{b}$同向,則$\overrightarrow{a}$>$\overrightarrow{b}$ | B. | 當實數λ=0時,λ$\overrightarrow{a}$=0 | ||
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | D. | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
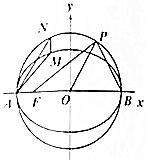 已知橢圓C1:$\frac{{x}^{2}}{4}$+y2=1和圓C2:x2+y2=4,A,B,F分別為橢圓C1左頂點、右頂點和左焦點.
已知橢圓C1:$\frac{{x}^{2}}{4}$+y2=1和圓C2:x2+y2=4,A,B,F分別為橢圓C1左頂點、右頂點和左焦點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com