
【題目】某網紅直播平臺為確定下一季度的廣告投入計劃,收集了近6個月廣告投入量![]() (單位:萬元)和收益
(單位:萬元)和收益![]() (單位:萬元)的數據如下表:
(單位:萬元)的數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
廣告投入量/萬元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/萬元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用兩種模型①![]() ,②
,②![]() 分別進行擬合,得到相應的回歸方程并進行殘差分析,得到如圖所示的殘差圖及一些統計量的值:
分別進行擬合,得到相應的回歸方程并進行殘差分析,得到如圖所示的殘差圖及一些統計量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
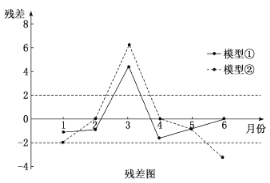
(1)根據殘差圖,比較模型①,②的擬合效果,應選擇哪個模型?并說明理由.
(2)殘差絕對值大于2的數據被認為是異常數據,需要剔除:
(i)剔除的異常數據是哪一組?
(ii)剔除異常數據后,求出(1)中所選模型的回歸方程;
(iii)廣告投入量![]() 時,(ii)中所得模型收益的預報值是多少?
時,(ii)中所得模型收益的預報值是多少?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: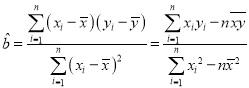 ,
,![]() .
.
【答案】(1)模型①,理由見解析;(2)(i)是3月份的數據; (ii)![]() ; (iii)62.04萬元.
; (iii)62.04萬元.
【解析】
(1)根據殘差圖中體現出的殘差點分布,結合其均勻程度以及帶狀區域的寬窄,即可分析比較;
(2)(i)根據題意,結合殘差圖,即可求得![]() 月份的數據異常,應該剔除;
月份的數據異常,應該剔除;
(ii)根據已知數據和![]() 月份的數據,結合
月份的數據,結合![]() 和
和![]() 的計算公式,即可求得結果;
的計算公式,即可求得結果;
(iii)令![]() ,代入(ii)中所求回歸直線方程,即可求得結果.
,代入(ii)中所求回歸直線方程,即可求得結果.
(1)應該選擇模型①,因為模型①的殘差點比較均勻地落在水平的帶狀區域中,
且模型①的帶狀區域比模型②的帶狀區域窄,
所以模型①的擬合精度高,回歸方程的預報精度高.
(2)(i)剔除異常數據是3月份的數據,即![]() ;
;
(ii)剔除異常數據,即3月份的數據后,得
![]() ,
,
![]()
![]() ,
,
![]() .
.
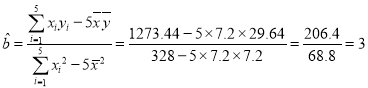 ,
,![]() .
.
所以![]() 關于
關于![]() 的回歸方程為
的回歸方程為![]() .
.
(iii)把![]() 代入(i)中所求回歸方程得
代入(i)中所求回歸方程得
![]() ,
,
故預報值為62.04萬元.


科目:高中數學 來源: 題型:
【題目】已知2件次品和3件正品混放在一起,現需要通過檢測將其區分,每次隨機檢測一件產品,檢測后不放回,直到檢測出2件次品或者檢測出3件正品時檢測結束.
(1)求第一次檢測出的是次品且第二次檢測出的是正品的概率;
(2)已知每檢測一件產品需要費用50元,設![]() 表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求
表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 是邊長為4的正方形,平面
是邊長為4的正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)求二面角![]() 的余弦值;
的余弦值;
(2)在線段![]() 是否存在點
是否存在點![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設自然數![]() 。求證:全體不大于n的合數可重新排列(不一定按原來的大小順序排列),使得每三個依次相鄰的數都有大于1的公因數(例如,當
。求證:全體不大于n的合數可重新排列(不一定按原來的大小順序排列),使得每三個依次相鄰的數都有大于1的公因數(例如,當![]() 時,排列
時,排列![]() 就滿足要求)。
就滿足要求)。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() ,設離心率為
,設離心率為![]() ,且滿足
,且滿足![]() ,其中
,其中![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)過點(0,1)的直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學的父親決定今年夏天賣西瓜賺錢,根據去年6月份的數據統計連續五天內每天所賣西瓜的個數與溫度之間的關系如下表:
溫度 | 32 | 33 | 35 | 37 | 38 |
西瓜個數 | 20 | 22 | 24 | 30 | 34 |
(1)求這五天內所賣西瓜個數的平均值和方差;
(2)求變量![]() 之間的線性回歸方程,并預測當溫度為
之間的線性回歸方程,并預測當溫度為![]() 時所賣西瓜的個數.
時所賣西瓜的個數.
附: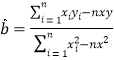 ,
,![]() (精確到
(精確到![]() ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com