
【題目】設自然數![]() 。求證:全體不大于n的合數可重新排列(不一定按原來的大小順序排列),使得每三個依次相鄰的數都有大于1的公因數(例如,當
。求證:全體不大于n的合數可重新排列(不一定按原來的大小順序排列),使得每三個依次相鄰的數都有大于1的公因數(例如,當![]() 時,排列
時,排列![]() 就滿足要求)。
就滿足要求)。
 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.離散型隨機變量![]() 的方差
的方差![]() 反映了隨機變量
反映了隨機變量![]() 取值的波動情況;
取值的波動情況;
B.隨機變量![]() ,其中
,其中![]() 越小,曲線越“矮胖”;
越小,曲線越“矮胖”;
C.若![]() 與
與![]() 是相互獨立事件,則
是相互獨立事件,則![]() 與
與![]() 也是相互獨立事件;
也是相互獨立事件;
D.從10個紅球和20個白球除顏色外完全相同中,一次摸出5個球,則摸到紅球的個數服從超幾何分布;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直線PB與CD所成角的大小為![]() ,求BC的長;
,求BC的長;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】稱直角坐標系中縱橫坐標均為整數的 點為“格點”,稱一格點沿坐標線到原點的最短路程為該點到原點的“格點距離”,格點距離為定值的點的軌跡稱為“格點圓”,該定值稱為格點圓的半徑,而每一條最短路程稱為一條半徑.當格點半徑為2005時,格點圓的半徑有________條.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,若普通6座以下私家車投保交強險第一年的費用 (基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,保費是與上一年度車輛發生道路交通安全違法行為或者道路交通事故的情況相聯系的.交強險第二年價格計算公式具體如下:交強險最終保費
元,在下一年續保時,實行的是費率浮動機制,保費是與上一年度車輛發生道路交通安全違法行為或者道路交通事故的情況相聯系的.交強險第二年價格計算公式具體如下:交強險最終保費![]() 基準保費
基準保費![]() (
(![]() 浮動比率
浮動比率![]() ).發生交通事故的次數越多,出險次數的就越多,費率也就越髙,具體浮動情況如下表:
).發生交通事故的次數越多,出險次數的就越多,費率也就越髙,具體浮動情況如下表:

某機構為了研究某一品牌普通6座以下私家車的投保情況,為此搜集并整理了100輛這一品牌普通6座以下私家車一年內的出險次數,得到下面的柱狀圖:

已知小明家里有一輛該品牌普通6座以下私家車且需要續保,續保費用為![]() 元.
元.
(1)記![]() 為事件“
為事件“![]() ”,求
”,求![]() 的估計值;
的估計值;
(2)求![]() 的平均估計值.
的平均估計值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網紅直播平臺為確定下一季度的廣告投入計劃,收集了近6個月廣告投入量![]() (單位:萬元)和收益
(單位:萬元)和收益![]() (單位:萬元)的數據如下表:
(單位:萬元)的數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
廣告投入量/萬元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/萬元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用兩種模型①![]() ,②
,②![]() 分別進行擬合,得到相應的回歸方程并進行殘差分析,得到如圖所示的殘差圖及一些統計量的值:
分別進行擬合,得到相應的回歸方程并進行殘差分析,得到如圖所示的殘差圖及一些統計量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
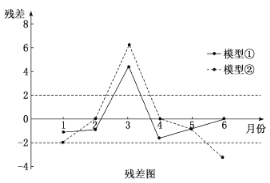
(1)根據殘差圖,比較模型①,②的擬合效果,應選擇哪個模型?并說明理由.
(2)殘差絕對值大于2的數據被認為是異常數據,需要剔除:
(i)剔除的異常數據是哪一組?
(ii)剔除異常數據后,求出(1)中所選模型的回歸方程;
(iii)廣告投入量![]() 時,(ii)中所得模型收益的預報值是多少?
時,(ii)中所得模型收益的預報值是多少?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: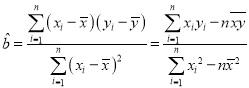 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,
中,![]() ,D為AB上一點,且
,D為AB上一點,且![]() 平面
平面![]() .
.
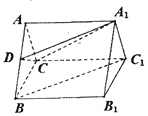
(1)求證:![]() ;
;
(2)若四邊形![]() 是矩形,且平面
是矩形,且平面![]() 平面ABC,直線
平面ABC,直線![]() 與平面ABC所成角的正切值等于2,
與平面ABC所成角的正切值等于2,![]() ,
,![]() ,求三樓柱
,求三樓柱![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某社團有男生30名,女生20名,從中抽取一個容量為5的樣本,恰好抽到2名男生和3名女生.有以下3種說法:
①該抽樣可能是簡單隨機抽樣;
②該抽樣不可能是分層隨機抽樣;
③該抽樣中,男生被抽到的概率大于女生被抽到的概率.
其中說法正確的為( )
A.①②③B.①②C.②③D.①③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com