
| A. | 22 | B. | 48 | C. | $\sqrt{46}$ | D. | 32 |
分析 根據題意和結論:$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,利用向量數量積的運算求出$|\overrightarrow{a}-\overrightarrow{b}|$的值.
解答 解:∵$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,
且$|{\overrightarrow a}|=13$,$|{\overrightarrow b}|=19$,$|{\overrightarrow a+\overrightarrow b}|=24$,
∴$|\overrightarrow{a}-\overrightarrow{b}|$=$\sqrt{2(1{3}^{2}+1{9}^{2})-2{4}^{2}}$=22,
故選A.
點評 本題考查了向量的模的結論:$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,以及向量數量積的應用,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{2}$ | B. | $2\sqrt{5}$ | C. | $\sqrt{17}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
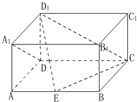 如圖,在長方體ABCD-A1B1C1D1中,AD=DD1=1,DC=2,E為AB上一點.
如圖,在長方體ABCD-A1B1C1D1中,AD=DD1=1,DC=2,E為AB上一點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
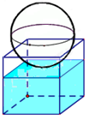 如圖是一個水平放置的透明無蓋的正方體容器,高12cm,將一個球放在容器口,再向容器內注水,當球面恰好接觸水面時測得水深為8cm,如果不計容器的厚度,則球的體積為( )
如圖是一個水平放置的透明無蓋的正方體容器,高12cm,將一個球放在容器口,再向容器內注水,當球面恰好接觸水面時測得水深為8cm,如果不計容器的厚度,則球的體積為( )| A. | $\frac{169π}{6}$cm3 | B. | $\frac{676π}{3}$cm3 | C. | $\frac{8788π}{3}$cm3 | D. | $\frac{2197π}{6}$cm3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $x=\frac{π}{3}$ | B. | $x=\frac{2π}{3}$ | C. | $x=\frac{5π}{12}$ | D. | $x=\frac{7π}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
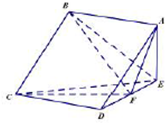 如圖,在四棱錐E-ABCD中,底面ABCD為正方形,AE⊥平面CDE,已知AE=DE=1,F為線段DE中點.
如圖,在四棱錐E-ABCD中,底面ABCD為正方形,AE⊥平面CDE,已知AE=DE=1,F為線段DE中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com