
分析 (I)對任意n∈N*,都有an2=2Sn-an,n=1時,${a}_{1}^{2}=2{a}_{1}-{a}_{1}$,a1>0,解得a1.n≥2時,${a}_{n-1}^{2}$=2Sn-1-an-1,相減可得:an-an-1=1.
(II)bn=2n+λ•3${\;}^{{a}_{n}}$=2n+λ•3n,假設使得對任意n∈N*,都有bn+1<bn成立,化為:λ<-$\frac{1}{2}(\frac{2}{3})^{n}$,利用數列的單調性即可得出.
解答 解:(I)∵對任意n∈N*,都有an2=2Sn-an,n=1時,${a}_{1}^{2}=2{a}_{1}-{a}_{1}$,a1>0,解得a1=1.
n≥2時,${a}_{n-1}^{2}$=2Sn-1-an-1,可得an2-${a}_{n-1}^{2}$=2Sn-an-(2Sn-1-an-1),an+an-1>0,化為:an-an-1=1.
∴an=1+(n-1)=n.
(II)bn=2n+λ•3${\;}^{{a}_{n}}$=2n+λ•3n,
假設使得對任意n∈N*,都有bn+1<bn成立,
則2n+1+λ•3n+1<2n+λ•3n,
化為:λ<-$\frac{1}{2}(\frac{2}{3})^{n}$,
∵數列$\{-\frac{1}{2}(\frac{2}{3})^{n}\}$單調遞增,
∴λ<$-\frac{1}{3}$.
∴λ的取值范圍是$(-∞,-\frac{1}{3})$.
點評 本題考查了等差數列的通項公式、數列遞推關系、數列的單調性、不等式的性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 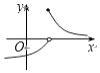 | B. | 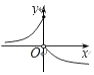 | C. | 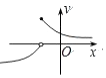 | D. | 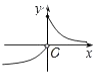 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
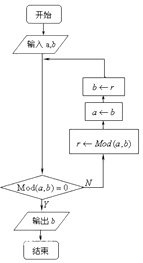 輾轉相除法,又名歐幾里得算法,乃求兩個正整數之最大公因子的算法.它是已知最古老的算法,在中國則可以追溯至東漢出現的《九章算術》,圖中的程序框圖所表述的算法就是歐幾里得輾轉相除法,若輸入a=5280,b=12155,則輸出的b=55.
輾轉相除法,又名歐幾里得算法,乃求兩個正整數之最大公因子的算法.它是已知最古老的算法,在中國則可以追溯至東漢出現的《九章算術》,圖中的程序框圖所表述的算法就是歐幾里得輾轉相除法,若輸入a=5280,b=12155,則輸出的b=55.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $4+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3+\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com