
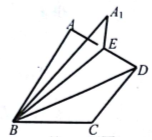
 如圖,在直二面角A-BD-C中,△ABD、△CBD均是以BD為斜邊的等腰直角三角形,取AD中點E,將△ABE沿BE翻折到△A1BE,在△ABE的翻折過程中,下列不可能成立的是( )
如圖,在直二面角A-BD-C中,△ABD、△CBD均是以BD為斜邊的等腰直角三角形,取AD中點E,將△ABE沿BE翻折到△A1BE,在△ABE的翻折過程中,下列不可能成立的是( )| A. | BC與平面A1BE內某直線平行 | B. | CD∥平面A1BE | ||
| C. | BC與平面A1BE內某直線垂直 | D. | BC⊥A1B |
分析 構造平面BCE,平面BFE,則可判斷A,B,C,使用假設法判斷D.
解答  解:連結CE,當平面A1BE與平面BCE重合時,BC?平面A1BE,
解:連結CE,當平面A1BE與平面BCE重合時,BC?平面A1BE,
∴平面A1BE內必存在與BC平行和垂直的直線,故A,C可能成立;
在平面BCD內過B作CD的平行線BF,使得BF=CD,
連結EF,則當平面A1BE與平面BEF重合時,BF?平面A1BE,
故平面A1BE內存在與BF平行的直線,即平面A1BE內存在與CD平行的直線,
∴CD∥平面A1BE,故C可能成立.
若BC⊥A1B,又A1B⊥A1E,則A1B為直線A1E和BC的公垂線,
∴A1B<CE,
設A1B=1,則經計算可得CE=$\frac{\sqrt{3}}{2}$,
與A1B<CE矛盾,故D不可能成立.
故選D.
點評 本題考查了空間線面位置關系的判斷,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | ±1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{2}$或$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | $\frac{24}{25}$ | C. | $\frac{16}{25}$ | D. | $\frac{24}{25}$或$\frac{16}{25}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com