
| 視覺 聽覺 | 視覺記憶能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 聽覺 記憶 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 | b | |
| 偏高 | 2 | a | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
分析 (1)由表格數據可知,視覺記憶能力恰為中等且聽覺記憶能力為中等或中等以上的學生共有(10+a)人,記“視覺記憶能力恰為中等且聽覺記憶能力為中等閾 中等以上”為事件A,由等可能事件概率計算公式能求出a=6,從而得到b=2.
(2)由于從40位學生中任取3位,其中具有聽覺記憶能力或視覺記憶能力偏高或超常的學生共有24人,故概率為$\frac{3}{5}$,從而ξ~B(3,$\frac{3}{5}$),由此能求出結果.
解答 解:(1)由表格數據可知,視覺記憶能力恰為中等且聽覺記憶能力為中等或中等以上的學生共有(10+a)人,
記“視覺記憶能力恰為中等且聽覺記憶能力為中等閾 中等以上”為事件A,
則P(A)=$\frac{10+a}{40}=\frac{2}{5}$,解得a=6,
∴b=40-(32+a)=40-38=2.
∴a=6,b=2.
(2)由于從40位學生中任取3位,其中具有聽覺記憶能力或視覺記憶能力偏高或超常的學生共有24人,
故概率為$\frac{3}{5}$,
∴從該地區高二年級學生中任意抽取3人,
其中恰有k位學生具有聽覺記憶能力或視覺記憶能力偏高或超常的概率P(ξ=k)=${C}_{3}^{k}(\frac{3}{5})^{k}(\frac{2}{5})^{3-k}$,(k=0,1,2,3),
ξ的可能取值為0,1,2,3,
P(ξ=0)=($\frac{2}{5}$)3=$\frac{8}{125}$,
P(ξ=1)=${C}_{3}^{1}(\frac{3}{5})(\frac{2}{5})^{2}=\frac{36}{125}$,
P(ξ=2)=${C}_{3}^{2}(\frac{3}{5})^{2}(\frac{2}{5})=\frac{54}{125}$,
P(ξ=3)=($\frac{3}{5}$)3=$\frac{27}{125}$,
∴ξ的分布列為:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{8}{125}$ | $\frac{36}{125}$ | $\frac{54}{125}$ | $\frac{27}{125}$ |
點評 本題考查概率的求法,考查離散型隨機變量的分布列和數學期望的求法,是基礎題,解題時要認真審題,注意二項分布的性質的合理運用.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
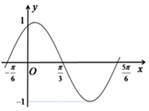 如圖是函數y=Asin(ωx+φ)(x∈R)在區間[-$\frac{π}{6}$,$\frac{5π}{6}$]上的圖象.為了得到這個函數的圖象,只需將y=sinx(x∈R)的圖象上所有的點( )
如圖是函數y=Asin(ωx+φ)(x∈R)在區間[-$\frac{π}{6}$,$\frac{5π}{6}$]上的圖象.為了得到這個函數的圖象,只需將y=sinx(x∈R)的圖象上所有的點( )| A. | 向左平移$\frac{π}{3}$個單位,再把所得各點的橫坐標縮短到原來的$\frac{1}{2}$倍 | |
| B. | 向左平移$\frac{π}{3}$個單位,再把所得各點的橫坐標伸長到原來的2倍 | |
| C. | 向左平移$\frac{π}{6}$個單位,再把所得各點的橫坐標縮短到原來的$\frac{1}{2}$倍 | |
| D. | 向左平移$\frac{π}{6}$個單位,再把所得各點的橫坐標伸長到原來的2倍 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
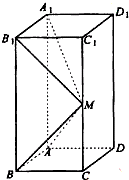 如圖所示,在長方體ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中點,
如圖所示,在長方體ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中點,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com