
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
分析 根據題意可得|$\overrightarrow{a}$|=2$\sqrt{2}$|$\overrightarrow{b}$|,且|$\overrightarrow{b}$-$\overrightarrow{a}$|=$\sqrt{3}$|$\overrightarrow{b}$|,再根據cos<$\overrightarrow a$,$\overrightarrow b$-$\overrightarrow a$>=$\frac{\overrightarrow{a}•(\overrightarrow{b}-\overrightarrow{a})}{|\overrightarrow{a}|•|\overrightarrow{b}-\overrightarrow{a}|}$,計算求的結果.
解答 解:非零向量$\overrightarrow a$,$\overrightarrow b$滿足$\overrightarrow a$⊥$\overrightarrow b$,∴$\overrightarrow{a}•\overrightarrow{b}$=0,
∵|$\overrightarrow a$+$\overrightarrow b$|=3|$\overrightarrow b$|,∴${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=9${\overrightarrow{b}}^{2}$,即${\overrightarrow{a}}^{2}$=8${\overrightarrow{b}}^{2}$,
∴|$\overrightarrow{a}$|=2$\sqrt{2}$|$\overrightarrow{b}$|.
∴|$\overrightarrow{b}$-$\overrightarrow{a}$|=3|$\overrightarrow{b}$|,
則cos<$\overrightarrow a$,$\overrightarrow b$-$\overrightarrow a$>=$\frac{\overrightarrow{a}•(\overrightarrow{b}-\overrightarrow{a})}{|\overrightarrow{a}|•|\overrightarrow{b}-\overrightarrow{a}|}$=$\frac{{-\overrightarrow{a}}^{2}}{2\sqrt{2}•|\overrightarrow{b}|•3|\overrightarrow{b}|}$
=$\frac{-{8\overrightarrow{b}}^{2}}{6\sqrt{2}{•|\overrightarrow{b}|}^{2}}$=-$\frac{2\sqrt{2}}{3}$,
故選:C.
點評 本題考查向量的夾角公式,考查向量的數量積的性質:斜率的平方即為模的平方,考查運算能力,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | [-2,1] | B. | (-2,1) | C. | (-2,1] | D. | {-2,1} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
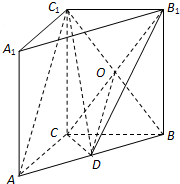 (理科做)如圖,在直三棱柱ABC-A1B1C1中,AC⊥BC,點D是AB的中點.
(理科做)如圖,在直三棱柱ABC-A1B1C1中,AC⊥BC,點D是AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|1<x≤6} | B. | {1,2,3,4,5,6} | C. | {2,3,4,5,6} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com