
分析 (1)利用向量共線定理即可得出.
(2)利用向量垂直與數(shù)量積的關系、數(shù)量積運算性質(zhì)即可得出.
解答 解:(1)因為$\overrightarrow a+k\overrightarrow c=(3,2)+k(4,1)=(3+4k,2+k)$,$2\overrightarrow b-\overrightarrow a=(-5,2)$,
又$(\overrightarrow a+k\overrightarrow c)∥(2\overrightarrow b-\overrightarrow a)$,
∴-5(2+k)=2(3+4k),解得k=-$\frac{16}{13}$.
(2)∵$\overrightarrow{a}+\overrightarrow{b}$=(2,4),$\overrightarrowp9vv5xb5-\overrightarrow{c}$=(x-4,y-1),
又$(\overrightarrow a+\overrightarrow b)⊥(\overrightarrow d-\overrightarrow c)$,$|\overrightarrow d-\overrightarrow c|=\sqrt{5}$,
∴$\left\{\begin{array}{l}{2(x-4)+4(y-1)=0}\\{(x-4)^{2}+(y-1)^{2}=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=6}\\{y=0}\end{array}\right.$,或$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
故$\overrightarrowp9vv5xb5$=(6,0)或(2,2).
點評 本題考查了向量共線定理、向量垂直與數(shù)量積的關系、數(shù)量積運算性質(zhì),考查了推理能力與計算能力,屬于基礎題.


 新思維假期作業(yè)寒假吉林大學出版社系列答案
新思維假期作業(yè)寒假吉林大學出版社系列答案科目:高中數(shù)學 來源: 題型:選擇題
| A. | 3+$\sqrt{5}$ | B. | 5+$\sqrt{5}$ | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 2 | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
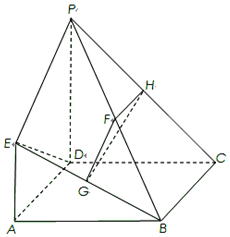 如圖,已知四邊形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F(xiàn),G,H分別為BP,BE,PC的中點.
如圖,已知四邊形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F(xiàn),G,H分別為BP,BE,PC的中點.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com