
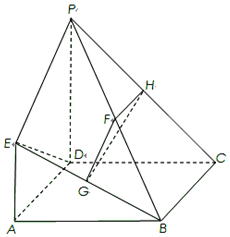
 如圖,已知四邊形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F(xiàn),G,H分別為BP,BE,PC的中點(diǎn).
如圖,已知四邊形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F(xiàn),G,H分別為BP,BE,PC的中點(diǎn).分析 (1)證明PD⊥BD,PC⊥BC,根據(jù)直角三角形的中線特點(diǎn)得出F為外接球的球心,計(jì)算出球的半徑代入面積公式計(jì)算即可;
(2)證明BC⊥平面ABE,F(xiàn)H∥BC即可得出FH⊥平面ABE,于是平面FGH⊥平面AEB;
(3)證明EF⊥PB,故只需FM⊥PB即可,利用相似三角形計(jì)算出PM.
解答 解:(1)連結(jié)FD,F(xiàn)C,
∵EA⊥平面ABCD,PD∥EA,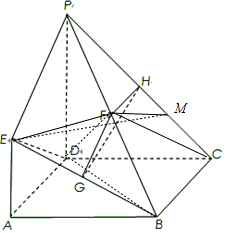
∴PD⊥平面ABCD,又BD?平面ABCD,
∴PD⊥BD,∵F是PB的中點(diǎn),
∴DF=$\frac{1}{2}$PB,
同理可得FC=$\frac{1}{2}$PB,
∴F為棱錐P-BCD的外接球的球心.
∵AD=PD=2EA=2,
∴BD=2$\sqrt{2}$,PB=$\sqrt{P{D}^{2}+B{D}^{2}}$=2$\sqrt{3}$,
∴四棱錐P-BCD外接球的表面積為4π•($\frac{2\sqrt{3}}{2}$)2=12π.
(2)證明:∵EA⊥平面ABCD,BC?平面ABCD,
∴EA⊥CB.又CB⊥AB,AB∩AE=A,
∴CB⊥平面ABE.
∵F,H分別為線段PB,PC的中點(diǎn),
∴FH∥BC.
∴FH⊥平面ABE.又FH?平面FGH,
∴平面FGH⊥平面ABE.
(3)在直角三角形AEB中,∵AE=1,AB=2,∴$BE=\sqrt{5}$.
在直角梯形EADP中,∵AE=1,AD=PD=2,∴$PE=\sqrt{5}$,
∴PE=BE.又F為PB的中點(diǎn),
∴EF⊥PB.
假設(shè)在線段PC上存在一點(diǎn)M,使PB⊥平面EFM.
只需滿足PB⊥FM即可,
∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥CB,又CB⊥CD,PD∩CD=D,
∴CB⊥平面PCD,∵PC?平面PCD,
∴CB⊥PC.若PB⊥FM,則△PFM∽△PCB,∴$\frac{PM}{PB}=\frac{PF}{PC}$.
∵$PB=2\sqrt{3}$,$PF=\sqrt{3}$,$PC=2\sqrt{2}$,
∴$PM=\frac{{3\sqrt{2}}}{2}$.
∴線段PC上存在一點(diǎn)M,使PB⊥平面EFM,此時PM=$\frac{3\sqrt{2}}{2}$.
點(diǎn)評 本題考查了球與棱錐的位置關(guān)系,面面垂直的判定,線面垂直的判定,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
| 暈機(jī) | 不暈機(jī) | 總計(jì) | |
| 男乘客 | |||
| 女乘客 | |||
| 總計(jì) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | bf(lna)<af(lnb) | B. | bf(lna)=af(lnb) | ||
| C. | bf(lna)>af(lnb) | D. | bf(lna)與af(lnb)的大小不確定 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com