
分析 由已知不等式作出可行域,求得t=$\frac{y-1}{x+1}$的范圍,把$\frac{{{x^2}+{y^2}+2x-2y+2}}{xy-x+y-1}$轉化為含有t得代數式,再利用“對勾函數”的單調性求得答案.
解答 解:由2≤y≤4-x,x≥1,作出可行域如圖,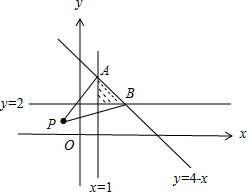
令t=$\frac{y-1}{x+1}$,其幾何意義為可行域內的動點(x,y)與定點P(-1,1)連線的斜率,
聯立$\left\{\begin{array}{l}{x=1}\\{y=4-x}\end{array}\right.$,解得A(1,3),
聯立$\left\{\begin{array}{l}{y=2}\\{y=4-x}\end{array}\right.$,解得B(2,2).
∵${k}_{PA}=\frac{3-1}{1-(-1)}=1$,${k}_{PB}=\frac{2-1}{2-(-1)}=\frac{1}{3}$.
∴t∈[$\frac{1}{3}$,1].
$\frac{{x}^{2}+{y}^{2}+2x-2y+2}{xy-x+y-1}=\frac{(x+1)^{2}+(y-1)^{2}}{(x+1)(y-1)}$
=$\frac{x+1}{y-1}+\frac{y-1}{x+1}$=$\frac{1}{t}+t$.
設f(t)=$\frac{1}{t}+t$,則由“對勾函數”的單調性可知,f(t)=$\frac{1}{t}+t$在[$\frac{1}{3}$,1]上為減函數,
∴當t=$\frac{1}{3}$時,$f(x)_{max}=3+\frac{1}{3}=\frac{10}{3}$.
故答案為:$\frac{10}{3}$.
點評 本題考查函數的最值及其幾何意義,考查簡單的線性規劃,訓練了利用“對勾函數”的單調性求函數的最值,是中檔題.


科目:高中數學 來源: 題型:解答題
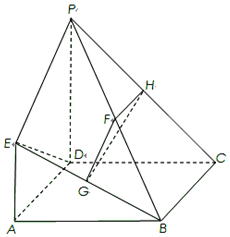 如圖,已知四邊形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分別為BP,BE,PC的中點.
如圖,已知四邊形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分別為BP,BE,PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 科幻片 | 文藝片 | 合計 | |
| 男 | |||
| 女 | |||
| 合計 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 年齡(單位:歲) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
| 贊成人數 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
| 贊成 | |||
| 不贊成 | |||
| 合計 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{4\sqrt{3}}}{5}$ | B. | $\frac{{3\sqrt{3}}}{5}$ | C. | $-\frac{{3\sqrt{3}}}{5}$ | D. | $-\frac{{4\sqrt{3}}}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com