Question

9．O為坐標原點，已知向量$\overrightarrow{OA}=（{1，5}），\overrightarrow{OB}=（{4，-1}），\overrightarrow{OC}=（{6，8}），x，y$為非負數實數，且0≤x+y≤1，$\overrightarrow{CD}=x\overrightarrow{CA}+y\overrightarrow{CB}$，則$|{\overrightarrow{OD}}|$的最小值為$\frac{7\sqrt{5}}{5}$．

Answer 1

分析 如圖所示，x，y非負數實數，且0≤x+y≤1，$\overrightarrow{CD}=x\overrightarrow{CA}+y\overrightarrow{CB}$，則點D表示的區域為△ABC及其內部的點．
當OD⊥AB時，$|{\overrightarrow{OD}}|$取得最小值．

解答 解：如圖所示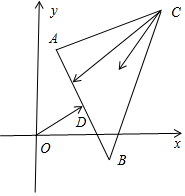，x，y非負數實數，且0≤x+y≤1，$\overrightarrow{CD}=x\overrightarrow{CA}+y\overrightarrow{CB}$，
則點D表示的區域為△ABC及其內部的點．
當OD⊥AB時，$|{\overrightarrow{OD}}|$取得最小值，
由直線AB的方程為：y+1=$\frac{-1-5}{4-1}$（x-4），
化為：2x+y-7=0．
∴則$|{\overrightarrow{OD}}|$的最小值=$\frac{|0-7|}{\sqrt{5}}$=$\frac{7\sqrt{5}}{5}$．
故答案為：$\frac{7\sqrt{5}}{5}$．

點評 本題考查了向量共線定理、平面向量基本定理、點到直線的距離公式，考查了推理能力與計算能力，屬于中檔題．