
分析 (1)將a=0代入f(x),求出f(x)的導數,得到函數的單調區間,從而求出函數的極小值即可;
(2)求出函數的導數,得到$-a≤\frac{1}{{{{ln}^2}x}}-\frac{1}{lnx}$,令lnx=t(t>0),得到$g(t)={(\frac{1}{t}-\frac{1}{2})^2}-\frac{1}{4}$,根據函數的單調性求出a的范圍即可;
(3)法一:通過討論a的范圍,判斷函數f(x)的單調性,從而確定a的范圍即可;法二:通過分離參數法求出a的范圍即可.
解答 解:(1)當a=0時,$f(x)=\frac{x}{lnx}$$f'(x)=\frac{lnx-1}{{{{ln}^2}x}}>0$…(1分)x>e
則f(x)在(0,e)為減函數,在(e,+∞)為增函數,…(3分)
所以f(x)極小值=f(e)=e…(4分)
(2)∵函數f(x)在(1,+∞)上為減函數,
∴$f'(x)=\frac{lnx-1}{{{{ln}^2}x}}-a≤0$在(1,+∞)上恒成立…(5分)
∴$-a≤\frac{1}{{{{ln}^2}x}}-\frac{1}{lnx}$,令lnx=t(t>0)…(6分)
$-a≤\frac{1}{t^2}-\frac{1}{t}$,令$g(t)={(\frac{1}{t}-\frac{1}{2})^2}-\frac{1}{4}$
則-a≤g(t)min…(7分)∴$-a≤-\frac{1}{4}$,則$a≥\frac{1}{4}$…(8分)
所以a的最小值為$\frac{1}{4}$…(9分)
(2)方法一、∵?x∈[e,e2],使f(x)≤$\frac{1}{4}$成立,
∴$f{(x)_{min}}≤\frac{1}{4}$…(10分)
1°$a≥\frac{1}{4}$,由(1)知f(x)在[e,e2]為減函數,
∴$f{(x)_{min}}=f({e^2})=\frac{e^2}{2}-a{e^2}≤\frac{1}{4}$,
∴$a≥\frac{1}{2}-\frac{1}{{4{e^2}}}$…(11分)
2°當$a<\frac{1}{4}$,$f'(x)=-{(\frac{1}{lnx}-\frac{1}{2})^2}+\frac{1}{4}-a$,
∵$e≤x≤{e^2}⇒1≤lnx≤2⇒\frac{1}{2}≤\frac{1}{lnx}≤1$$⇒-a≤f'(x)≤\frac{1}{4}-a$…(12分)
①當-a≥0,即a≤0f'(x)≥0在[e,e2]上恒成立,
則f(x)在[e,e2]為增函數,
∴f(x)min=f(e)=e-ae≤$\frac{1}{4}$
則$a≥1-\frac{1}{4e}$(不合題意)…(13分)
②當$-a<0⇒0<a<\frac{1}{4}$$?{x_0}∈(e,{e^2}),f'({x_0})=0$,
則$f(x)在(e,{x_0})上為減函數,在({x_0},{e^2})上為增函數$,
∴$f{(x)_{min}}=f({x_0})=\frac{x_0}{{ln{x_0}}}-a{x_0}≤\frac{1}{4}$,
∴$a≥\frac{1}{{ln{x_0}}}-\frac{1}{{4{x_0}}}>\frac{1}{{ln{e^2}}}-\frac{1}{4e}=\frac{1}{2}-\frac{1}{4e}>\frac{1}{4}$(不合題意)…(15分)
綜上所述:$a≥\frac{1}{2}-\frac{1}{{4{e^2}}}$…(16分)
方法二、由題意:$?x∈[e,{e^2}],\frac{x}{lnx}-ax≤\frac{1}{4}$
等價于$?x∈[e,{e^2}],a≥\frac{1}{lnx}-\frac{1}{4x}$…(10分)
∴$a≥{(\frac{1}{lnx}-\frac{1}{4x})_{min}}$,x∈[e,e2]…(11分)
令$φ(x)=\frac{1}{lnx}-\frac{1}{4x}$
則$φ'(x)=-\frac{1}{{x{{ln}^2}x}}+\frac{1}{{4{x^2}}}=\frac{{{{ln}^2}x-4x}}{{4{x^2}{{ln}^2}x}}$…(12分)
∵e≤x≤e2⇒1≤lnx≤2⇒1≤ln2x≤44e≤4x≤4e2⇒-4e2≤4x≤-4e,
∴1-4e2≤ln2x-4x≤4-4e<0,
∴φ'(x)<0⇒φ(x)在[e,e2]上為減函數,…(14分)
∴$φ{(x)_{min}}=φ({e^2})=\frac{1}{{ln{e^2}}}-\frac{1}{4e}=\frac{1}{2}-\frac{1}{4e}$…(15分)
∴$a≥\frac{1}{2}-\frac{1}{{4{e^2}}}$…(16分)
點評 本題考查了函數的單調性、最值、極值問題,考查導數的應用以及分類討論思想,考查轉化思想以及函數恒成立問題,是一道中檔題.


 目標測試系列答案
目標測試系列答案科目:高中數學 來源: 題型:解答題
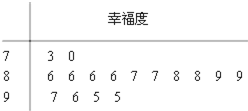 某權威機構發布了2014年度“城市居民幸福排行榜”,某市成為本年度城市最“幸福城”.隨后,該市某校學生會組織部分同學,用“10分制”隨機調查“陽光”社區人們的幸福度.現從調查人群中隨機抽取16名,如圖所示的莖葉圖記錄了他們的幸福度分數(以小數點前的一位數字為莖,小數點后的一位數字為葉):
某權威機構發布了2014年度“城市居民幸福排行榜”,某市成為本年度城市最“幸福城”.隨后,該市某校學生會組織部分同學,用“10分制”隨機調查“陽光”社區人們的幸福度.現從調查人群中隨機抽取16名,如圖所示的莖葉圖記錄了他們的幸福度分數(以小數點前的一位數字為莖,小數點后的一位數字為葉):查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
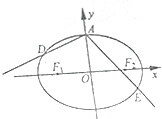 如圖,橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,長軸長為2$\sqrt{2}$,左、右焦點分別為F1,F2,上頂點為A.
如圖,橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,長軸長為2$\sqrt{2}$,左、右焦點分別為F1,F2,上頂點為A.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
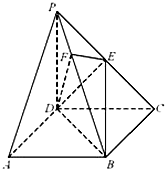 《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.
《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com