Question

13．如圖，已知長方形ABCD中，AB=2$\sqrt{2}$，AD=$\sqrt{2}$，M為DC的中點．將△ADM沿AM折起，使得平面ADM⊥平面ABCM．
（1）求證：AD⊥BM；
（2）求直線DB與平面ABCM所成角的正弦值．

Answer 1

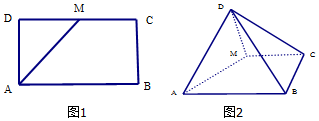
分析 （1）在長方形ABCD中，可得AM=BM=2，BM⊥AM，
即BM⊥平面ADM，AD⊥BM；           
（2）取AM得中點N，連接DH，BH，MB
則DH⊥AM，又平面ADM⊥平面ABCM，∴DH⊥面ABCM，DH⊥HB
故∠DBH即為直線DB與平面ABCM所成角
在Rt△DHB中，求解直線DB與平面ABCM所成角的正弦值

解答 （1）證明：∵長方形ABCD中，AB=$2\sqrt{2}$，AD=$\sqrt{2}$，M為DC的中點，
∴AM=BM=2，∴BM⊥AM．∵平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，BM?平面ABCM
∴BM⊥平面ADM；∵AD?平面ADM∴AD⊥BM；                 …（6分）
（2）取AM得中點N，連接DH，BH，MB
則DH⊥AM，又平面ADM⊥平面ABCM，∴DH⊥面ABCM，DH⊥HB
故∠DBH即為直線DB與平面ABCM所成角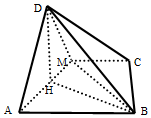

在Rt△DAM中，DH=$\frac{1}{2}AM=1$，
由（1）得BM⊥平面ADM，BM⊥DM
∴$DB=\sqrt{B{M}^{2}+D{M}^{2}}=\sqrt{6}$
在Rt△DHB中，sin$∠DBH=\frac{DH}{DB}=\frac{1}{\sqrt{6}}=\frac{\sqrt{6}}{6}$
∴直線DB與平面ABCM所成角的正弦值為$\frac{\sqrt{6}}{6}$

點評 本題考查了空間線線垂直的判定，線面角的求解，考查了轉化思想，屬于中檔題．