
| A. | 39 | B. | 45 | C. | 50 | D. | 55 |
分析 推導出{$\sqrt{{a}_{n}+1}$}是首項為1,公差為1的等差數列,從而${a}_{n}={n}^{2}-1$,由此能求出a5+S4的值.
解答 解:∵數列{an}的前n和為Sn,a1=0,an+1=an+2$\sqrt{{a}_{n}+1}$+1,
∴$\sqrt{{a}_{n+1}+1}-\sqrt{{a}_{n}+1}$=1,$\sqrt{{a}_{1}+1}=0$,
∴{$\sqrt{{a}_{n}+1}$}是首項為1,公差為1的等差數列,
∴$\sqrt{{a}_{n}+1}$=1+(n-1)×1=n,
∴${a}_{n}={n}^{2}-1$,
∴${a}_{5}={5}^{2}-1$=24,
${S}_{4}={1}^{2}+{2}^{2}+{3}^{2}+{4}^{2}-4$=26.
∴a5+S4=24+26=50.
故選:C.
點評 本題考查數列的前5項和的求法,是基礎題,解題時要認真審題,注意構造法的合理運用.


科目:高中數學 來源: 題型:選擇題
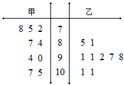 某次運動會甲、乙兩名射擊運動員成績如圖所示,甲、乙的平均數分別為為 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分別為s甲2,s乙2,則( )
某次運動會甲、乙兩名射擊運動員成績如圖所示,甲、乙的平均數分別為為 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分別為s甲2,s乙2,則( )| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2>s乙2 | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2<s乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2>s乙2 | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2<s乙2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}π{R^2}$ | B. | $\frac{{\sqrt{3}}}{2}π{R^2}$ | C. | πR2 | D. | $\frac{3}{4}π{R^2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{72}{13}$ | B. | $\frac{135}{22}$ | C. | $\frac{79}{14}$ | D. | $\frac{142}{23}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2$\sqrt{3}$] | B. | [2,+∞) | C. | (-∞,-2$\sqrt{3}$]∪[2$\sqrt{3}$,+∞) | D. | (-∞,-2$\sqrt{3}$)∪(2$\sqrt{3}$,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com