
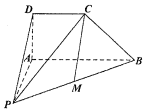
 如圖,在四棱錐P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.
如圖,在四棱錐P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.分析 (1)取AP的中點N,連接MN和DN,利用中位線定理得出四邊形MNDC時平行四邊形,故而CM∥DN,從而CM∥平面PAD;
(2)利用勾股定理的逆定理證明AC⊥BC,結合BC⊥PC得出BC⊥平面PAC,于是平面PAC⊥平面PBC.
解答 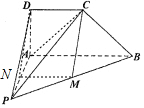 證明:(1)取AP的中點N,連接MN和DN,
證明:(1)取AP的中點N,連接MN和DN,
∵M是PB的中點,N是PA的中點,
∴$MN∥AB,MN=\frac{1}{2}AB$,
又$CD∥AB,CD=\frac{1}{2}AB$,
∴MN=CD,MN∥CD,
∴四邊形MNDC是平行四邊形,
∴CM∥DN.
又CM?平面PAD,DN?平面PAD,
∴CM∥平面PAD.
(2)設AD=CD=1,則AB=2,
∴AC=$\sqrt{2}$,BC=$\sqrt{2}$,
∴AC2+BC2=AB2,∴BC⊥AC,
又BC⊥PC,AC?平面ACP,PC?面ACP,AC∩PC=C,
∴BC⊥面ACP,又BC?面PBC,
∴平面PAC⊥平面PBC.
點評 本題考查了線面平行的判定,面面垂直的判定,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {y|0<y<$\frac{1}{2}$} | B. | {y|0<y<1} | C. | {y|$\frac{1}{2}$<y<1} | D. | ∅ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,2) | B. | [1,2] | C. | (1,3) | D. | (1,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\frac{6}{2×{3}^{2016}-1}$ | C. | $\frac{2}{2×{3}^{2016}-1}$ | D. | $\frac{2}{2×{3}^{2015}-1}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com