
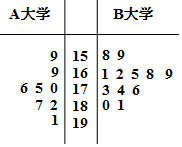
 某市旅游節需在A大學和B大學中分別招募8名和12名志愿者,這20名志愿者的身高(單位:cm)繪制出如圖所示的莖葉圖.若身高在175cm以上(包括175cm)定義為“高個子”,身高在175cm以下(不包括175cm)定義為“非高個子”,且只有B大學的“高個子”才能擔任“兼職導游”.
某市旅游節需在A大學和B大學中分別招募8名和12名志愿者,這20名志愿者的身高(單位:cm)繪制出如圖所示的莖葉圖.若身高在175cm以上(包括175cm)定義為“高個子”,身高在175cm以下(不包括175cm)定義為“非高個子”,且只有B大學的“高個子”才能擔任“兼職導游”.分析 (1)由莖葉圖可知,“高個子”有8人,“非高個子”有12人,從而可得5人中“高個子”為2人,“非高個子”為3人,從而可求至少有1人為高個子的概率P=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{7}{10}$; (2)由題意可知:ξ的可能取值為0,1,2,3,求出相應的概率,可得ξ的分布列與數學期望.
解答 解:(1)由莖葉圖可知,“高個子”有8人,“非高個子”有12人,
∴按照分層抽樣抽取的5人中“高個子”為5×$\frac{8}{20}$=2人,“非高個子”為5×$\frac{12}{20}$=3人,
則至少有1人為高個子的概率P=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{7}{10}$,
至少有1人是“高個子”的概率是$\frac{7}{10}$;
(2)由題可知:B大學的高個子只有3人,則ξ的可能取值為0,1,2,3;
故P(ξ=0)=$\frac{{C}_{5}^{3}}{{C}_{8}^{3}}$=$\frac{10}{56}$=$\frac{5}{28}$,P(ξ=1)=$\frac{{C}_{5}^{2}{C}_{3}^{1}}{{C}_{8}^{3}}$=$\frac{30}{56}$=$\frac{15}{28}$,P(ξ=2)=$\frac{{C}_{5}^{1}{C}_{3}^{2}}{{C}_{8}^{3}}$=$\frac{15}{56}$,P(ξ=3)=$\frac{{C}_{3}^{3}}{{C}_{8}^{3}}$=$\frac{1}{56}$,
即ξ的分布列為:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{5}{28}$ | $\frac{15}{28}$ | $\frac{15}{56}$ | $\frac{1}{56}$ |
點評 本題考查莖葉圖的應用,考查離散型隨機變量的分布列與數學期望,考查計算能力,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | B. | y=x0與g(x)=$\frac{1}{{x}^{0}}$ | ||
| C. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2n-1 | B. | 2n+1-2 | C. | ${2^{\frac{n}{2}}}-\sqrt{2}$ | D. | ${2^{\frac{n-2}{2}}}-\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com