

���� ��1���C��CD��ƽ��DBE�������C��CD��BE��
��2����?y��n)龀��BE��BF�ڷ����^�����L�Ȳ�׃������(j��)���ɶ�����$\left\{{\begin{array}{l}{B{E^2}=B{H^2}+E{H^2}}\\{B{F^2}=B{H^2}+F{H^2}=B{H^2}+F{G^2}+G{H^2}}\end{array}}\right.⇒\left\{{\begin{array}{l}{5={h^2}+{k^2}}\\{9={2^2}+{h^2}+{{��2-k��}^2}}\end{array}}\right.$���ɽ��$\left\{{\begin{array}{l}{h=2}\\{k=1}\end{array}}\right.$��������BH���L�ȣ�
��3������c(di��n)A��ƽ��EFCD�ľ��x��$\frac{2}{3}$����$AF=\sqrt{13}$��������ֱ��AF�cƽ��EFCD���ɽǵ�����ֵ��
��� ��1���C��������BH��ƽ��CDEF����BH��CD��
������CD��DE��BH��DE=H��
��CD��ƽ��DBE����CD��BE��
��2���⣺�O(sh��)BH=h��EH=k���^F��FG��ֱED���c(di��n)G��
��?y��n)龀��BE��BF�ڷ����^�����L�Ȳ�׃������(j��)���ɶ�����$\left\{{\begin{array}{l}{B{E^2}=B{H^2}+E{H^2}}\\{B{F^2}=B{H^2}+F{H^2}=B{H^2}+F{G^2}+G{H^2}}\end{array}}\right.⇒\left\{{\begin{array}{l}{5={h^2}+{k^2}}\\{9={2^2}+{h^2}+{{��2-k��}^2}}\end{array}}\right.$���ɽ��$\left\{{\begin{array}{l}{h=2}\\{k=1}\end{array}}\right.$��
�ྀ��BH���L�Ȟ�2��
��3���⣺���LBA��EF���c(di��n)M��
��AE��BF=MA��MB=1��3�����c(di��n)A��ƽ��EFCD�ľ��x���c(di��n)B��ƽ��EFCD���x��$\frac{1}{3}$��
���c(di��n)A��ƽ��EFCD�ľ��x��$\frac{2}{3}$����$AF=\sqrt{13}$��
��ֱ��AF�cƽ��EFCD���ɽǵ�����ֵ��$\frac{{2\sqrt{13}}}{39}$��
�c(di��n)�u ���}����ֱ���cƽ�洹ֱ���C�������龀��ǵĴ�С�������}�rҪ�J(r��n)�挏�}��ע����g˼�S���������B(y��ng)��


 ������Ӌ��С��Ԫϵ�д�
������Ӌ��С��Ԫϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ��x���}
| A�� | ��$\sqrt{2}$��+�ޣ� | B�� | ��1��$\sqrt{2}$+1�� | C�� | ��2��+�ޣ� | D�� | ��1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ��x���}
| A�� | $\frac{{\sqrt{5}-1}}{2}$ | B�� | $\frac{{\sqrt{5}+1}}{2}$ | C�� | $\sqrt{5}+1$ | D�� | $\sqrt{5}-1$ |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ��x���}
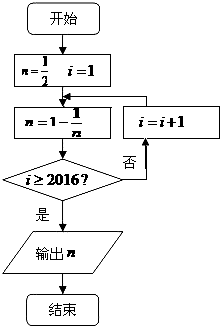
| A�� | -1 | B�� | 1 | C�� | $\frac{1}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com