
| A. | 50 | B. | 45 | C. | 36 | D. | 35 |
分析 根據題意,按個位數字的不同分9種情況討論,分別求出每一種情況的符合條件的兩位數數目,由分類計數原理計算可得答案.
解答 解:根據題意,按個位數字的不同分9種情況討論:
①、當個位數字為0時,其十位數字可以為1、2、3、4、5、6、7、8、9,共9種情況;
②、當個位數字為1時,其十位數字可以為2、3、4、5、6、7、8、9,共8種情況;
③、當個位數字為2時,其十位數字可以為3、4、5、6、7、8、9,共7種情況;
④、當個位數字為3時,其十位數字可以為4、5、6、7、8、9,共6種情況;
⑤、當個位數字為4時,其十位數字可以為5、6、7、8、9,共5種情況;
⑥、當個位數字為5時,其十位數字可以為6、7、8、9,共4種情況;
⑦、當個位數字為6時,其十位數字可以為7、8、9,共3種情況;
⑧、當個位數字為7時,其十位數字可以為8、9,共2種情況;
⑨、當個位數字為8時,其十位數字可以為9,共1種情況;
則十位數字大于個位數字的兩位數共有9+8+7+6+5+4+3+2+1=45個;
故答案為:45.
點評 本題考查分類計數原理的應用,注意“十位數字大于個位數字”與“十位數字小于個位數字”的個數不等,不能用倍分法分析.


科目:高中數學 來源: 題型:選擇題
| A. | $(\frac{3π}{16},\frac{11π}{16})$ | B. | $(\frac{π}{16},\frac{9π}{16})$ | C. | $(-\frac{3π}{16},\frac{5π}{16})$ | D. | $(\frac{π}{16},\frac{5π}{16})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
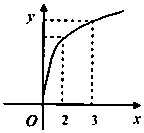 函數f(x)的圖象如圖所示,f′(x)是f(x)的導函數,則下列數值排序正確的是( )
函數f(x)的圖象如圖所示,f′(x)是f(x)的導函數,則下列數值排序正確的是( )| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f′(3)<f(3)-f(2)<f′(2) | C. | 0<f′(3)<f′(2)<f(3)-f(2) | D. | 0<f(3)-f(2)<f′(2)<f′(3) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| x | 1 | 2 | 3 |
| y | 5 | 4 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com