
分析 (1)通過將an-1-an=4an-1•an兩邊同時除以an-1•an、進而可知數列$\left\{{\frac{1}{a_n}}\right\}$是首項為5、公差為4的等差數列,利用等差數列的通項公式計算可得結論;
(2)通過(1)裂項可知bn=$\frac{1}{4}$($\frac{1}{4n+1}$-$\frac{1}{4n+5}$),進而并項相加放縮可得結論.
解答 證明:(1)因為an-1-an-4an-1•an=0,
所以an-1-an=4an-1•an,
兩邊同時除以an-1•an得:$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=4,
又因為$\frac{1}{{a}_{1}}$=5,
所以數列$\left\{{\frac{1}{a_n}}\right\}$是首項為5、公差為4的等差數列,
所以$\frac{1}{{a}_{n}}$=5+4(n-1)=4n+1,
所以an=$\frac{1}{4n+1}$;
(2)由(1)可知bn=an•an+1=$\frac{1}{4n+1}$•$\frac{1}{4n+5}$=$\frac{1}{4}$($\frac{1}{4n+1}$-$\frac{1}{4n+5}$),
所以Sn=$\frac{1}{4}$($\frac{1}{5}$-$\frac{1}{9}$+$\frac{1}{9}$-$\frac{1}{13}$+…+$\frac{1}{4n+1}$-$\frac{1}{4n+5}$)=$\frac{1}{4}$($\frac{1}{5}$-$\frac{1}{4n+5}$)<$\frac{1}{20}$,
即${S_n}<\frac{1}{20}$.
點評 本題是一道關于數列與不等式的綜合題,考查數列的通項及前n項和,考查裂項相消法,對表達式的靈活變形是解決本題的關鍵,注意解題方法的積累,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | [-2,2] | B. | [-1,1] | C. | [0,4] | D. | [1,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1盞 | B. | 3盞 | C. | 5盞 | D. | 9盞 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
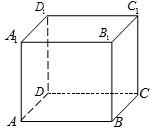 在正方體ABCD-A1B1C1D1中,給出下列結論:
在正方體ABCD-A1B1C1D1中,給出下列結論:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x=$\frac{2}{3}$π | B. | x=-$\frac{1}{12}$π | C. | x=$\frac{1}{3}$π | D. | x=$\frac{5}{12}$π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com