
分析 求得切線方程,分別令x=0,求得B點坐標,當y=0時,求得A點坐標,根據(jù)三角形的面積公式,即可求得與兩坐標軸圍成的三角形面積為定值.
解答  解:證明:設曲線$y=\frac{1}{x}$上任意一點為P(x0,$\frac{1}{{x}_{0}}$),∵y′=-$\frac{1}{{x}^{2}}$,
解:證明:設曲線$y=\frac{1}{x}$上任意一點為P(x0,$\frac{1}{{x}_{0}}$),∵y′=-$\frac{1}{{x}^{2}}$,
∴在點P處切線的斜率k=-$\frac{1}{{x}_{0}^{2}}$,
∴在P點處的切線方程為y-$\frac{1}{{x}_{0}}$=-$\frac{1}{{x}_{0}^{2}}$(x-x0).
令x=0,得y=$\frac{1}{{x}_{0}}$+$\frac{1}{{x}_{0}}$=$\frac{2}{{x}_{0}}$,則B(0,$\frac{2}{{x}_{0}}$)
令y=0,得x=x0+x02×$\frac{1}{{x}_{0}}$=2x0,C(2x0,0),
∴S△=$\frac{1}{2}$|x|•|y|=2.
故三角形面積為定值2.
過P處的切線與與兩坐標軸圍成的三角形面積為定值2.
點評 本題考查利用導數(shù)求函數(shù)的切線方程,考查計算能力,屬于基礎題.


 百年學典課時學練測系列答案
百年學典課時學練測系列答案 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
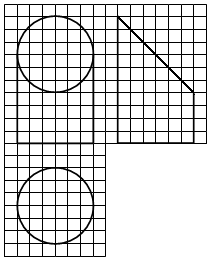 如圖,網格紙上小正方形的邊長為1,粗實線畫出的是某幾何體的三視圖,該幾何體由一平面將一圓柱截去一部分后所得,則該幾何體的體積為( )
如圖,網格紙上小正方形的邊長為1,粗實線畫出的是某幾何體的三視圖,該幾何體由一平面將一圓柱截去一部分后所得,則該幾何體的體積為( )| A. | 90π | B. | 63π | C. | 42π | D. | 36π |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com