
| A. | 若q>1,則數列{Tn}單調遞增 | B. | 若數列{Tn}單調遞增,則q>1 | ||
| C. | 若Tn>0,則數列{Tn}單調遞增 | D. | 若數列{Tn}單調遞增,則Tn>0 |
分析 根據題意,結合等比數列的性質,依次分析選項,綜合即可得答案.
解答 解:根據題意,依次分析選項:
對于A、若等比數列{an}的公比為q>1,Tn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$,而當首項a1<0時,數列{Tn}不是單調遞減的,故A錯誤,
對于B、當等比數列{an}的首項a1>0,公比為q=1時,數列{Tn}單調遞增,故B錯誤,
對于C、當等比數列{an}的首項a1>0,公比為q=1時,Tn>0,故C錯誤,
對于D、若數列{Tn}單調遞增,則有an=Tn-Tn-1>0,即等比數列{an}為正項數列,則Tn=a1+a2+a3+…+an>0,故D正確;
故選:D.
點評 本題考查等比數列的性質,關鍵是掌握等比數列的通項公式和前n項和公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $-\frac{4}{3}$ | D. | -3 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
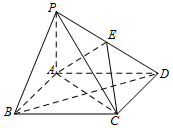 如圖,在四棱錐P-ABCD中,PA=AB=$\frac{1}{2}$AD=2,PB=2$\sqrt{2}$,PA⊥AD,底面ABCD為平行四邊形,∠ADC=60°,E為PD的中點.
如圖,在四棱錐P-ABCD中,PA=AB=$\frac{1}{2}$AD=2,PB=2$\sqrt{2}$,PA⊥AD,底面ABCD為平行四邊形,∠ADC=60°,E為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | C. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com