
分析 根據(jù)向量的坐標(biāo)運(yùn)算和向量投影的定義即可求出
解答 解:∵向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(2,3),
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(5,7),$\overrightarrow{a}$-$\overrightarrow{b}$=(1,1),
∴($\overrightarrow{a}$+$\overrightarrow{b}$)($\overrightarrow{a}$-$\overrightarrow{b}$)=57=12,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{2}$,
∴$\overrightarrow{a}$+$\overrightarrow{b}$在$\overrightarrow{a}$-$\overrightarrow{b}$方向上的投影為$\frac{(\overrightarrow{a}+\overrightarrow{b})(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{12}{\sqrt{2}}$=6$\sqrt{2}$,
故答案為:6$\sqrt{2}$.
點(diǎn)評(píng) 本題考查了向量的坐標(biāo)運(yùn)算和向量投影的定義,屬于基礎(chǔ)題



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
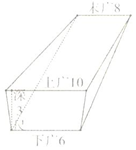 《九章算術(shù)》是東方數(shù)學(xué)思想之源,在卷五《商功》中有以下問題:今有羨除,下廣六尺,上廣一丈,深三尺,末廣八尺,無深,袤七尺,問積幾何?譯文:如圖所示的幾何體是三個(gè)側(cè)面皆為等腰梯形,其他兩面為直角三角形的五面體,(前端)下寬6尺,上寬一丈,深3尺,末端寬8尺,無深,長7尺,則它的體積是84立方尺.
《九章算術(shù)》是東方數(shù)學(xué)思想之源,在卷五《商功》中有以下問題:今有羨除,下廣六尺,上廣一丈,深三尺,末廣八尺,無深,袤七尺,問積幾何?譯文:如圖所示的幾何體是三個(gè)側(cè)面皆為等腰梯形,其他兩面為直角三角形的五面體,(前端)下寬6尺,上寬一丈,深3尺,末端寬8尺,無深,長7尺,則它的體積是84立方尺.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
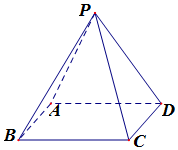 如圖在四棱錐P-ABCD中,底面ABCD為矩形,側(cè)面PAD⊥底面ABCD,PA⊥PC;
如圖在四棱錐P-ABCD中,底面ABCD為矩形,側(cè)面PAD⊥底面ABCD,PA⊥PC;查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3,-3 | B. | 1,-3 | C. | 1,-1 | D. | 3,-1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 若q>1,則數(shù)列{Tn}單調(diào)遞增 | B. | 若數(shù)列{Tn}單調(diào)遞增,則q>1 | ||
| C. | 若Tn>0,則數(shù)列{Tn}單調(diào)遞增 | D. | 若數(shù)列{Tn}單調(diào)遞增,則Tn>0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
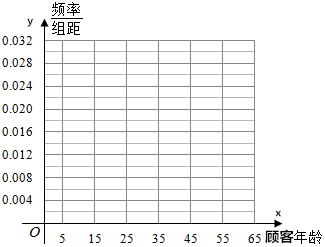 某電商在6月18日之后,隨機(jī)抽取100名顧客進(jìn)行回訪,按顧客的年齡分成6組,得到如下頻數(shù)分布表:
某電商在6月18日之后,隨機(jī)抽取100名顧客進(jìn)行回訪,按顧客的年齡分成6組,得到如下頻數(shù)分布表:| 顧客年齡 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 頻數(shù) | 4 | 24 | 32 | 20 | 16 | 4 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com