
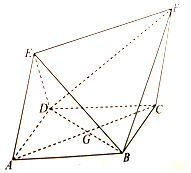
 如圖,四邊形ABCD為菱形,四邊形ACEF為平行四邊形,設(shè)BD與AC相交于點G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如圖,四邊形ABCD為菱形,四邊形ACEF為平行四邊形,設(shè)BD與AC相交于點G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.分析 (1)連接EG,說明BD⊥AC,證明BD⊥EG,推出BD⊥平面ACFE,然后證明平面ACEF⊥平面ABCD;
(2)說明點F到平面BDE的距離為點C到平面BDE的距離的兩倍,利用VF-BDE=2VC-BDE,轉(zhuǎn)化求解三棱錐F-BDE的體積即可.
解答 解:(1)證明: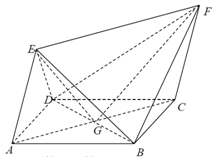
連接EG,
∵四邊形ABCD為菱形,
∵AD=AB,BD⊥AC,DG=GB,
在△EAD和△EAB中,
AD=AB,AE=AE,∠EAD=∠EAB,
∴△EAD≌△EAB,
∴ED=EB,
∴BD⊥EG,
∵AC∩EG=G,
∴BD⊥平面ACFE,
∵BD?平面ABCD,
∴平面ACEF⊥平面ABCD;
(2)∵EF∥GC,EF=2GC,∴點F到平面BDE的距離為點C到平面BDE的距離的兩倍,
所以VF-BDE=2VC-BDE,
作EH⊥AC,∵平面ACEF⊥平面ABCD,EH⊥平面ABCD,
∴VC-BDE=VE-BCD=$\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\frac{3}{2}$=$\frac{\sqrt{3}}{2}$,
∴三棱錐F-BDE的體積為$\sqrt{3}$.
點評 本題考查直線與平面垂直的判定定理以及性質(zhì)定理的應(yīng)用,幾何體的體積的求法,考查空間想象能力以及計算能力.


 鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學(xué)出版社系列答案
鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學(xué)出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
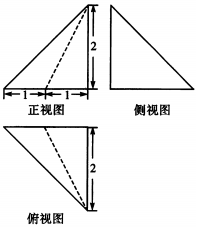
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{{1+\sqrt{3}}}{2}$ | B. | 2 | C. | 4 | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com