
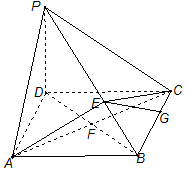
 如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,四邊形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一點.
如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,四邊形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一點.分析 (1)連接BD,設AC與BD相交于點F,推導出AC⊥BD,PD⊥AC,從而AC⊥平面PDB,由此能證明AC⊥DE.
(2)連結EF,推導出AC⊥EF,EF⊥PB,PB⊥AC,從而PB⊥平面AEC,進而PB⊥EC,再求出EC⊥AE,由此能證明EC⊥平面PAB.
(3)求出EF=3作GH∥CE交PB于點G,推導出∠GEH就是EG與平面PAB所成角,由此能求出存在滿足題意的點G,且BG=4.
解答 證明:(1)連接BD,設AC與BD相交于點F
因為四邊形ABCD是菱形,所以AC⊥BD.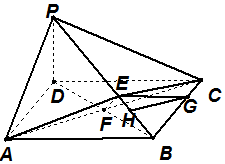
又∵PD⊥平面ABCD,AC?平面ABCD,∴PD⊥AC,
而PD∩BD=D,∴AC⊥平面PDB,
又∵DE?平面PBD,∴AC⊥DE.--------------(4分)
(2)連結EF,由(I)知AC⊥平面PDB,EF?平面PBD,
∴AC⊥EF.∵${S_{△ACE}}=\frac{1}{2}AC•EF$,且AC=6
當△ACE面積最小時,EF最小,這時EF⊥PB.-------(6分)
∵AC⊥平面PDB,∴PB⊥AC,
又∵EF∩AC=F,∴PB⊥平面AEC,∴PB⊥EC,----------------(7分)
又由 EF=AF=FC=3,可得 EC⊥AE,---------(8分)
而PB∩AE=E,
故EC⊥平面PAB.---------------------(9分)
解:(3)由已知,${({{S_{△ACE}}})_{min}}=\frac{1}{2}×6×EF=9$,解得EF=3
作GH∥CE交PB于點G,由(2)知EC⊥平面PAB,
∴GH⊥平面PAB,
∴∠GEH就是EG與平面PAB所成角,----------------------(12分)
在直角三角形CEB中,$BC=6,\;EC=3\sqrt{2}\;,\;EB=3\sqrt{2}$
∴∠CBE=45°
設BG=x,則$BH=HG=\frac{{\sqrt{2}}}{2}x$.
由tan∠GEH=2得 $EH=\frac{{\sqrt{2}}}{4}x$.
由EH+HB=EB得 x=4
即存在滿足題意的點G,且BG=4.----------(14分)
點評 本題考查線線垂直的證明,考查線面垂直的證明,考查滿足條件的線段長的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


科目:高中數學 來源: 題型:選擇題
| A. | 1組 | B. | 2組 | C. | 3組 | D. | 4組 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-1,0)∪(0,\frac{1}{2})$ | B. | $(-\frac{1}{2},0)∪(0,1)$ | C. | $(-1,\frac{1}{2})$ | D. | $(-\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 20 | B. | 24 | C. | 32 | D. | 40 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 年齡(歲) | 30 | 35 | 40 | 45 | 50 |
| 健康消費(百元) | 5 | 8 | 10 | 14 | 18 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | -3 | C. | $\frac{7}{3}$ | D. | -$\frac{7}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com