
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,對一切
,對一切![]() ,點
,點![]() 都在函數
都在函數![]() 的圖象上.
的圖象上.
(1)求![]() ,歸納數列
,歸納數列![]() 的通項公式(不必證明).
的通項公式(不必證明).
(2)將數列![]() 依次按1項、2項、3項、4項循環地分為
依次按1項、2項、3項、4項循環地分為![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為
,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為![]() ,求
,求![]() 的值.
的值.
(3)設![]() 為數列
為數列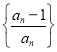 的前
的前![]() 項積,且
項積,且![]() ,求數列
,求數列![]() 的最大項.
的最大項.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)2010;(3)
;(2)2010;(3)![]() .
.
【解析】
(1)化簡得到![]() ,計算
,計算![]() ,
,![]() ,
,![]() ,猜想
,猜想![]() 得到答案.
得到答案.
(2)計算![]() ,再計算
,再計算![]() ,相加得到答案.
,相加得到答案.
(3)計算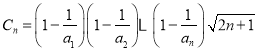 ,故
,故![]() ,故
,故![]() 是單調遞減,計算
是單調遞減,計算![]() 得到答案.
得到答案.
(1)因為點![]() 在函數
在函數![]() 的圖象上,故
的圖象上,故![]() ,所以
,所以![]() .令
.令![]() ,得
,得![]() ,所以
,所以![]() ;
;
令![]() ,得
,得![]() ,所以
,所以![]() ;
;
令![]() ,得
,得![]() ,所以
,所以![]() ;
;
由此猜想:![]() .
.
(2)因為![]() ,所以數列
,所以數列![]() 依次按1項、2項、3項、4項循環地分為
依次按1項、2項、3項、4項循環地分為![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,
每一次循環記為一組.由于每一個循環含有4個括號,
故![]() 是第25組中第4個括號內各數之和.
是第25組中第4個括號內各數之和.
由分組規律知,由各組第4個括號中所有第1個數組成的數列是等差數列,且公差為20.
同理,由各組第4個括號中所有第2個數、所有第3個數、所有第4個數分別組成的數列也都是等差數列,且公差均為20.
故各組第4個括號中各數之和構成等差數列,且公差為80.
注意到第一組中第4個括號內各數之和是68,所以![]() .
.
又![]() ,所以
,所以![]() .
.
(3)因為![]() ,故
,故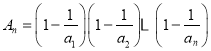 ,
,
所以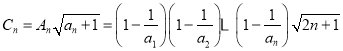 .
.
由于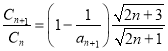
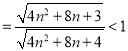 ,
,
所以![]() ,故
,故![]() 是單調遞減,
是單調遞減,
于是數列![]() 的最大項為
的最大項為![]() .
.


科目:高中數學 來源: 題型:
【題目】[選修4—4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的方程為
的方程為![]() .以坐標原點為極點,
.以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 有且僅有三個公共點,求
有且僅有三個公共點,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為![]() ,過點
,過點![]() 的直線l的參數方程為
的直線l的參數方程為 (為參數),直線l與曲線C交于M、N兩點。
(為參數),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標方程:
(2)若![]() 成等比數列,求a的值。
成等比數列,求a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一個四位數的各位數字相加和為10,則稱該數為“完美四位數”,如數字“2017”.試問用數字0,1,2,3,4,5,6,7組成的無重復數字且大于2017的“完美四位數”有( )個.
A. 71B. 66C. 59D. 53
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著現代社會的發展,我國對于環境保護越來越重視,企業的環保意識也越來越強.現某大型企業為此建立了5套環境監測系統,并制定如下方案:每年企業的環境監測費用預算定為1200萬元,日常全天候開啟3套環境監測系統,若至少有2套系統監測出排放超標,則立即檢查污染源處理系統;若有且只有1套系統監測出排放超標,則立即同時啟動另外2套系統進行1小時的監測,且后啟動的這2套監測系統中只要有1套系統監測出排放超標,也立即檢查污染源處理系統.設每個時間段(以1小時為計量單位)被每套系統監測出排放超標的概率均為![]() ,且各個時間段每套系統監測出排放超標情況相互獨立.
,且各個時間段每套系統監測出排放超標情況相互獨立.
(1)當![]() 時,求某個時間段需要檢查污染源處理系統的概率;
時,求某個時間段需要檢查污染源處理系統的概率;
(2)若每套環境監測系統運行成本為300元/小時(不啟動則不產生運行費用),除運行費用外,所有的環境監測系統每年的維修和保養費用需要100萬元.現以此方案實施,問該企業的環境監測費用是否會超過預算(全年按9000小時計算)?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農戶考察三種不同的果樹苗A、B、C,經引種試驗后發現,引種樹苗A的自然成活率為0.8,引種樹苗B、C的自然成活率均為0.9.
(1)若引種樹苗A、B、C各10棵.
①估計自然成活的總棵數;
②利用①的估計結論,從沒有自然成活的樹苗中隨機抽取兩棵,求抽到的兩棵都是樹苗A的概率;
(2)該農戶決定引種B種樹苗,引種后沒有自然成活的樹苗中有75%的樹苗可經過人工栽培技術處理,處理后成活的概率為0.8,其余的樹苗不能成活.若每棵樹苗引種最終成活后可獲利300元,不成活的每棵虧損50元,該農戶為了獲利不低于20萬元,問至少引種B種樹苗多少棵?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動圓![]() 與
與![]() 相外切,與
相外切,與![]() 相內切.
相內切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)![]() 是動圓
是動圓![]() 的半徑最小時的圓,傾斜角為
的半徑最小時的圓,傾斜角為![]() 且過點
且過點![]() 的直線l與
的直線l與![]() 相切,與軌跡
相切,與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生物興趣小組對冬季晝夜溫差與反季節新品種大豆發芽數之間的關系進行研究,他們分別記錄了![]() 月
月![]() 日至
日至![]() 月
月![]() 日每天的晝夜溫差與實驗室每天
日每天的晝夜溫差與實驗室每天![]() 顆種子的發芽數,得到以下表格
顆種子的發芽數,得到以下表格

該興趣小組確定的研究方案是:先從這![]() 組數據中選取
組數據中選取![]() 組數據,然后用剩下的
組數據,然后用剩下的![]() 組數據求線性回歸方程,再用被選取的
組數據求線性回歸方程,再用被選取的![]() 組數據進行檢驗.
組數據進行檢驗.
(1) 求統計數據中發芽數的平均數與方差;
(2) 若選取的是![]() 月
月![]() 日與
日與![]() 月
月![]() 日的兩組數據,請根據
日的兩組數據,請根據![]() 月
月![]() 日至
日至![]() 月
月![]() 日的數據,求出發芽數
日的數據,求出發芽數![]() 關于溫差
關于溫差![]() 的線性回歸方程
的線性回歸方程![]() ,若由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差不超過
,若由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差不超過![]() ,則認為得到的線性回歸方程是可靠的,問得到的線性回歸方程是否可靠? 附:線性回歸方程
,則認為得到的線性回歸方程是可靠的,問得到的線性回歸方程是否可靠? 附:線性回歸方程![]() 中斜率和截距最小二乘估法計算公式:
中斜率和截距最小二乘估法計算公式:
 ,
, ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com