
【題目】動圓![]() 與
與![]() 相外切,與
相外切,與![]() 相內切.
相內切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)![]() 是動圓
是動圓![]() 的半徑最小時的圓,傾斜角為
的半徑最小時的圓,傾斜角為![]() 且過點
且過點![]() 的直線l與
的直線l與![]() 相切,與軌跡
相切,與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根據(jù)動圓![]() 與
與![]() 外切,與
外切,與![]() 內切,由橢圓定義可知,點
內切,由橢圓定義可知,點![]() 的軌跡是以
的軌跡是以![]() 、
、![]() 為焦點的橢圓;
為焦點的橢圓;
(2)由(1)知:![]() 要使半徑
要使半徑![]() 最小,則
最小,則![]() 最小,易知
最小,易知![]() ,
,
則可設直線方程為![]() ,根據(jù)直線與圓
,根據(jù)直線與圓![]() 相切求出參數(shù)
相切求出參數(shù)![]() 的值,即可得到直線方程,最后聯(lián)立直線與橢圓方程,利用弦長公式計算可得.
的值,即可得到直線方程,最后聯(lián)立直線與橢圓方程,利用弦長公式計算可得.
解:(1)設動圓![]() 的半徑為
的半徑為![]() ,則由題可知:
,則由題可知:![]() ,
,![]()
∴![]() ,
,
由橢圓定義可知點![]() 的軌跡是以
的軌跡是以![]() ,
,![]() 為焦點,
為焦點,
長軸為6的橢圓,![]() ,
,![]()
![]() ,
,![]() ,
,
![]() 的軌跡方程為:
的軌跡方程為:![]()
(2)由(1)知:![]() 要使半徑
要使半徑![]() 最小,
最小,
則![]() 最小,易知
最小,易知![]()
由于![]() ,
,![]() ,圓
,圓![]() 的方程為:
的方程為:![]()
又由題可得直線![]() 的方程為:
的方程為:![]() ,即
,即![]()
![]() 到直線
到直線![]() 的距離為:
的距離為:![]() ,
,![]() 或
或![]() (舍去)
(舍去)
∴直線![]() 的方程為:
的方程為:![]() ,聯(lián)立橢圓方程:
,聯(lián)立橢圓方程:![]() 消去
消去![]() 整理得:
整理得:
![]() ,設
,設![]() ,
,![]()
則![]() ,
,![]() ,
,
∴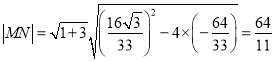 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】【選修4-4,坐標系與參數(shù)方程】
在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為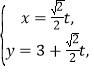 (t為參數(shù)),在以O為極點,
(t為參數(shù)),在以O為極點,![]() 軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為
軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為![]()
(Ⅰ)求直線![]() 的普通方程與曲線C的直角坐標方程;
的普通方程與曲線C的直角坐標方程;
(Ⅱ)若直線![]() 與
與![]() 軸的交點為P,直線
軸的交點為P,直線![]() 與曲線C的交點為A,B,求
與曲線C的交點為A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,對一切
,對一切![]() ,點
,點![]() 都在函數(shù)
都在函數(shù)![]() 的圖象上.
的圖象上.
(1)求![]() ,歸納數(shù)列
,歸納數(shù)列![]() 的通項公式(不必證明).
的通項公式(不必證明).
(2)將數(shù)列![]() 依次按1項、2項、3項、4項循環(huán)地分為
依次按1項、2項、3項、4項循環(huán)地分為![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分別計算各個括號內各數(shù)之和,設由這些和按原來括號的前后順序構成的數(shù)列為
,…,分別計算各個括號內各數(shù)之和,設由這些和按原來括號的前后順序構成的數(shù)列為![]() ,求
,求![]() 的值.
的值.
(3)設![]() 為數(shù)列
為數(shù)列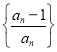 的前
的前![]() 項積,且
項積,且![]() ,求數(shù)列
,求數(shù)列![]() 的最大項.
的最大項.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【選修4-4,坐標系與參數(shù)方程】
在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為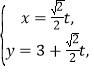 (t為參數(shù)),在以O為極點,
(t為參數(shù)),在以O為極點,![]() 軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為
軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為![]()
(Ⅰ)求直線![]() 的普通方程與曲線C的直角坐標方程;
的普通方程與曲線C的直角坐標方程;
(Ⅱ)若直線![]() 與
與![]() 軸的交點為P,直線
軸的交點為P,直線![]() 與曲線C的交點為A,B,求
與曲線C的交點為A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知橢圓C的方程為![]() ,設AB是過橢圓C中心O的任意弦,l是線段AB的垂直平分線,M是l上與O不重合的點.
,設AB是過橢圓C中心O的任意弦,l是線段AB的垂直平分線,M是l上與O不重合的點.
(1)求以橢圓的焦點為頂點,頂點為焦點的雙曲線方程;
(2)若![]() ,當點A在橢圓C上運動時,求點M的軌跡方程;
,當點A在橢圓C上運動時,求點M的軌跡方程;
(3)記M是l與橢圓C的交點,若直線AB的方程為![]() ,當
,當![]() 面積取最小值時,求直線AB的方程;
面積取最小值時,求直線AB的方程;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,且橢圓過點
,且橢圓過點![]()
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,
上,![]() 是坐標原點,若
是坐標原點,若![]() ,判定四邊形
,判定四邊形![]() 的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 為實數(shù),用
為實數(shù),用![]() 表示不超過
表示不超過![]() 的最大整數(shù),例如
的最大整數(shù),例如![]() ,
,![]() ,
,![]() .對于函數(shù)
.對于函數(shù)![]() ,若存在
,若存在![]() 且
且![]() ,使得
,使得![]() ,則稱函數(shù)
,則稱函數(shù)![]() 是“和諧”函數(shù).
是“和諧”函數(shù).
(1)判斷函數(shù)![]() ,
,![]() 是否是“和諧”函數(shù);(只需寫出結論)
是否是“和諧”函數(shù);(只需寫出結論)
(2)設函數(shù)![]() 是定義在
是定義在![]() 上的周期函數(shù),其最小周期為
上的周期函數(shù),其最小周期為![]() ,若
,若![]() 不是“和諧”函數(shù),求
不是“和諧”函數(shù),求![]() 的最小值.
的最小值.
(3)若函數(shù)![]() 是“和諧”函數(shù),求
是“和諧”函數(shù),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某芯片公司對今年新開發(fā)的一批5G手機芯片進行測評,該公司隨機調查了100顆芯片,并將所得統(tǒng)計數(shù)據(jù)分為![]() 五個小組(所調查的芯片得分均在
五個小組(所調查的芯片得分均在![]() 內),得到如圖所示的頻率分布直方圖,其中
內),得到如圖所示的頻率分布直方圖,其中![]() .
.
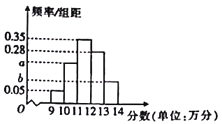
(1)求這100顆芯片評測分數(shù)的平均數(shù)(同一組中的每個數(shù)據(jù)可用該組區(qū)間的中點值代替).
(2)芯片公司另選100顆芯片交付給某手機公司進行測試,該手機公司將每顆芯片分別裝在3個工程手機中進行初測。若3個工程手機的評分都達到11萬分,則認定該芯片合格;若3個工程手機中只要有2個評分沒達到11萬分,則認定該芯片不合格;若3個工程手機中僅1個評分沒有達到11萬分,則將該芯片再分別置于另外2個工程手機中進行二測,二測時,2個工程手機的評分都達到11萬分,則認定該芯片合格;2個工程手機中只要有1個評分沒達到11萬分,手機公司將認定該芯片不合格.已知每顆芯片在各次置于工程手機中的得分相互獨立,并且芯片公司對芯片的評分方法及標準與手機公司對芯片的評分方法及標準都一致(以頻率作為概率).每顆芯片置于一個工程手機中的測試費用均為300元,每顆芯片若被認定為合格或不合格,將不再進行后續(xù)測試,現(xiàn)手機公司測試部門預算的測試經費為10萬元,試問預算經費是否足夠測試完這100顆芯片?請說明理由.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com