
【題目】某農戶考察三種不同的果樹苗A、B、C,經引種試驗后發現,引種樹苗A的自然成活率為0.8,引種樹苗B、C的自然成活率均為0.9.
(1)若引種樹苗A、B、C各10棵.
①估計自然成活的總棵數;
②利用①的估計結論,從沒有自然成活的樹苗中隨機抽取兩棵,求抽到的兩棵都是樹苗A的概率;
(2)該農戶決定引種B種樹苗,引種后沒有自然成活的樹苗中有75%的樹苗可經過人工栽培技術處理,處理后成活的概率為0.8,其余的樹苗不能成活.若每棵樹苗引種最終成活后可獲利300元,不成活的每棵虧損50元,該農戶為了獲利不低于20萬元,問至少引種B種樹苗多少棵?
【答案】(1)①26②![]() (2)該農戶至少種植700棵樹苗,就可獲利不低于20萬元
(2)該農戶至少種植700棵樹苗,就可獲利不低于20萬元
【解析】
(1)①用每種的棵樹10乘以對應的成活率再相加即可.
②根據古典概型的方法求解即可.
(2) 設該農戶種植B樹苗n棵,再根據題意求出獲利的解析式,再求解不等式即可.
解:(1)①依題意:
![]() ,
,
所以自然成活的總棵數為26.
②沒有自然成活的樹苗共4棵,其中兩棵A種樹苗、一棵B種樹苗、一棵C種樹苗,
分別設為![]() ,
,![]() ,b,c,
,b,c,
從中隨機抽取兩棵,可能的情況有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
抽到的兩棵都是樹苗A的概率為![]() .
.
(2)設該農戶種植B樹苗n棵,最終成活的棵數為![]() ,
,
未能成活的棵數為![]() ,
,
由題意知![]() ,則有
,則有![]() .
.
所以該農戶至少種植700棵樹苗,就可獲利不低于20萬元.


科目:高中數學 來源: 題型:
【題目】(卷號)2040818101747712
(題號)2050752239689728
(題文)
在平面直角坐標系中,以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系.已知直線![]() 的參數方程為
的參數方程為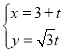 (
(![]() 為參數),曲線C的極坐標方程為
為參數),曲線C的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,點
兩點,點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是圓內接四邊形,
是圓內接四邊形,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)設線段![]() 的中點為
的中點為![]() ,線段
,線段![]() 的中點為
的中點為![]() ,且
,且![]() 在線段
在線段![]() 上運動,求直線
上運動,求直線![]() 與平面
與平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,對一切
,對一切![]() ,點
,點![]() 都在函數
都在函數![]() 的圖象上.
的圖象上.
(1)求![]() ,歸納數列
,歸納數列![]() 的通項公式(不必證明).
的通項公式(不必證明).
(2)將數列![]() 依次按1項、2項、3項、4項循環地分為
依次按1項、2項、3項、4項循環地分為![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為
,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為![]() ,求
,求![]() 的值.
的值.
(3)設![]() 為數列
為數列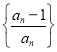 的前
的前![]() 項積,且
項積,且![]() ,求數列
,求數列![]() 的最大項.
的最大項.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為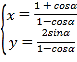 (
(![]() 為參數).以
為參數).以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ),將曲線
),將曲線![]() 向左平移2個單位長度得到曲線
向左平移2個單位長度得到曲線![]() .
.
(1)求曲線![]() 的普通方程和極坐標方程;
的普通方程和極坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4,坐標系與參數方程】
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為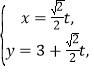 (t為參數),在以O為極點,
(t為參數),在以O為極點,![]() 軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為
軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為![]()
(Ⅰ)求直線![]() 的普通方程與曲線C的直角坐標方程;
的普通方程與曲線C的直角坐標方程;
(Ⅱ)若直線![]() 與
與![]() 軸的交點為P,直線
軸的交點為P,直線![]() 與曲線C的交點為A,B,求
與曲線C的交點為A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,且橢圓過點
,且橢圓過點![]()
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,
上,![]() 是坐標原點,若
是坐標原點,若![]() ,判定四邊形
,判定四邊形![]() 的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的偶函數
上的偶函數![]() 滿足
滿足![]() ,且
,且![]() ,當
,當![]() 時,
時,![]() .已知方程
.已知方程![]() 在區間
在區間![]() 上所有的實數根之和為
上所有的實數根之和為![]() .將函數
.將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象,則
的圖象,則![]() __________,
__________,![]() __________.
__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com