
【題目】隨著現代社會的發展,我國對于環境保護越來越重視,企業的環保意識也越來越強.現某大型企業為此建立了5套環境監測系統,并制定如下方案:每年企業的環境監測費用預算定為1200萬元,日常全天候開啟3套環境監測系統,若至少有2套系統監測出排放超標,則立即檢查污染源處理系統;若有且只有1套系統監測出排放超標,則立即同時啟動另外2套系統進行1小時的監測,且后啟動的這2套監測系統中只要有1套系統監測出排放超標,也立即檢查污染源處理系統.設每個時間段(以1小時為計量單位)被每套系統監測出排放超標的概率均為![]() ,且各個時間段每套系統監測出排放超標情況相互獨立.
,且各個時間段每套系統監測出排放超標情況相互獨立.
(1)當![]() 時,求某個時間段需要檢查污染源處理系統的概率;
時,求某個時間段需要檢查污染源處理系統的概率;
(2)若每套環境監測系統運行成本為300元/小時(不啟動則不產生運行費用),除運行費用外,所有的環境監測系統每年的維修和保養費用需要100萬元.現以此方案實施,問該企業的環境監測費用是否會超過預算(全年按9000小時計算)?并說明理由.
【答案】(1)![]() ;(2)不會超過預算,理由見解析
;(2)不會超過預算,理由見解析
【解析】
(1)求出某個時間段在開啟3套系統就被確定需要檢查污染源處理系統的概率為![]() ,某個時間段在需要開啟另外2套系統才能確定需要檢查污染源處理系統的概率為
,某個時間段在需要開啟另外2套系統才能確定需要檢查污染源處理系統的概率為![]() ,可得某個時間段需要檢查污染源處理系統的概率;
,可得某個時間段需要檢查污染源處理系統的概率;
(2)設某個時間段環境監測系統的運行費用為![]() 元,則
元,則![]() 的可能取值為900,1500.求得
的可能取值為900,1500.求得![]() ,
,![]() ,求得其分布列和期望
,求得其分布列和期望![]()
![]() ,對其求導,研究函數的單調性,可得期望的最大值,從而得出結論.
,對其求導,研究函數的單調性,可得期望的最大值,從而得出結論.
(1)![]() 某個時間段在開啟3套系統就被確定需要檢查污染源處理系統的概率為
某個時間段在開啟3套系統就被確定需要檢查污染源處理系統的概率為![]() ,
,
某個時間段在需要開啟另外2套系統才能確定需要檢查污染源處理系統的概率為
![]()
![]() 某個時間段需要檢查污染源處理系統的概率為
某個時間段需要檢查污染源處理系統的概率為![]() .
.
(2)設某個時間段環境監測系統的運行費用為![]() 元,則
元,則![]() 的可能取值為900,1500.
的可能取值為900,1500.
![]() ,
,![]()
![]()
![]()
令![]() ,則
,則![]()
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,
,![]() 在上
在上![]() 單調遞減,
單調遞減,
![]() 的最大值為
的最大值為![]() ,
,
![]() 實施此方案,最高費用為
實施此方案,最高費用為![]() (萬元),
(萬元),
![]() ,故不會超過預算.
,故不會超過預算.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源: 題型:
【題目】圓周率![]() 是一個在數學及物理學中普遍存在的數學常數,它既常用又神秘,古今中外很多數學家曾研究它的計算方法.下面做一個游戲:讓大家各自隨意寫下兩個小于1的正數然后請他們各自檢查一下,所得的兩數與1是否能構成一個銳角三角形的三邊,最后把結論告訴你,只需將每個人的結論記錄下來就能算出圓周率的近似值.假設有
是一個在數學及物理學中普遍存在的數學常數,它既常用又神秘,古今中外很多數學家曾研究它的計算方法.下面做一個游戲:讓大家各自隨意寫下兩個小于1的正數然后請他們各自檢查一下,所得的兩數與1是否能構成一個銳角三角形的三邊,最后把結論告訴你,只需將每個人的結論記錄下來就能算出圓周率的近似值.假設有![]() 個人說“能”,而有
個人說“能”,而有![]() 個人說“不能”,那么應用你學過的知識可算得圓周率
個人說“不能”,那么應用你學過的知識可算得圓周率![]() 的近似值為()
的近似值為()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 、…、
、…、![]() 為平面
為平面![]() 內的
內的![]() 個點,在平面
個點,在平面![]() 內的所有點中,若點
內的所有點中,若點![]() 到
到![]() 、
、![]() 、…、
、…、![]() 點的距離之和最小,則稱點
點的距離之和最小,則稱點![]() 為
為![]() 、
、![]() 、…、
、…、![]() 點的一個“中位點”,有下列命題:①
點的一個“中位點”,有下列命題:①![]() 、
、![]() 、
、![]() 三個點共線,
三個點共線,![]() 在線段
在線段![]() 上,則
上,則![]() 是
是![]() 、
、![]() 、
、![]() 的中位點;②直角三角形斜邊的中點是該直線三角形三個頂點的中位點;③若四個點
的中位點;②直角三角形斜邊的中點是該直線三角形三個頂點的中位點;③若四個點![]() 、
、![]() 、
、![]() 、
、![]() 共線,則它們的中位點存在且唯一;④梯形對角線的交點是該梯形四個頂點的唯一中位點;其中的真命題是( )
共線,則它們的中位點存在且唯一;④梯形對角線的交點是該梯形四個頂點的唯一中位點;其中的真命題是( )
A.②④B.①②C.①④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.設m為實數,若方程![]() 表示雙曲線,則m>2.
表示雙曲線,則m>2.
B.“p∧q為真命題”是“p∨q為真命題”的充分不必要條件
C.命題“x∈R,使得x2+2x+3<0”的否定是:“x∈R,x2+2x+3>0”
D.命題“若x0為y=f(x)的極值點,則f’(x)=0”的逆命題是真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,對一切
,對一切![]() ,點
,點![]() 都在函數
都在函數![]() 的圖象上.
的圖象上.
(1)求![]() ,歸納數列
,歸納數列![]() 的通項公式(不必證明).
的通項公式(不必證明).
(2)將數列![]() 依次按1項、2項、3項、4項循環地分為
依次按1項、2項、3項、4項循環地分為![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為
,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為![]() ,求
,求![]() 的值.
的值.
(3)設![]() 為數列
為數列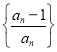 的前
的前![]() 項積,且
項積,且![]() ,求數列
,求數列![]() 的最大項.
的最大項.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為確定下一年度投入某種產品的生產所需的資金,需了解每投入2千萬資金后,工人人數![]() (單位:百人)對年產能
(單位:百人)對年產能![]() (單位:千萬元)的影響,對投入的人力和年產能的數據作了初步處理,得到散點圖和統計量表.
(單位:千萬元)的影響,對投入的人力和年產能的數據作了初步處理,得到散點圖和統計量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
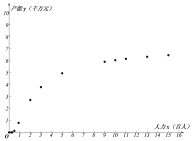
(1)根據散點圖判斷:![]() 與
與![]() 哪一個適宜作為年產能
哪一個適宜作為年產能![]() 關于投入的人力
關于投入的人力![]() 的回歸方程類型?并說明理由?
的回歸方程類型?并說明理由?
(2)根據(1)的判斷結果及相關的計算數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)現該企業共有2000名生產工人,資金非常充足,為了使得年產能達到最大值,則下一年度共需投入多少資金(單位:千萬元)?
附注:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為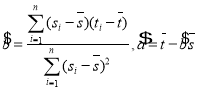 ,(說明:
,(說明:![]() 的導函數為
的導函數為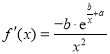 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知橢圓C的方程為![]() ,設AB是過橢圓C中心O的任意弦,l是線段AB的垂直平分線,M是l上與O不重合的點.
,設AB是過橢圓C中心O的任意弦,l是線段AB的垂直平分線,M是l上與O不重合的點.
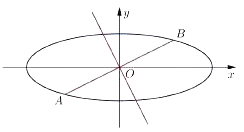
(1)求以橢圓的焦點為頂點,頂點為焦點的雙曲線方程;
(2)若![]() ,當點A在橢圓C上運動時,求點M的軌跡方程;
,當點A在橢圓C上運動時,求點M的軌跡方程;
(3)記M是l與橢圓C的交點,若直線AB的方程為![]() ,當
,當![]() 面積取最小值時,求直線AB的方程;
面積取最小值時,求直線AB的方程;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com