
分析 (Ⅰ)求導數,對 a分類討論,利用導數的正負,可得函數f(x)的單調區間;
(Ⅱ)求出函數的導數,解關于導函數的不等式,求出函數的單調區間,得到函數的最小值,從而證出結論即可.
解答 解:(Ⅰ)求導數可得f′(x)=$\frac{(x-a)(x-1)}{x}$(x>0)
(1)0<a<1時,令f′(x)<0,可得a<x<1,
∵x>0,∴a<x<1;令f′(x)>0,可得x<a或x>1,
∵x>0,∴0<x<a或x>1
∴函數f(x)在(0,a),(1,+∞)上單調遞增,在(a,1)上單調遞減;
(2)a=1時,f′(x)≥0,函數在(0,+∞)上單調遞增;
(3)a>1時,令f′(x)<0,可得1<x<a,
∵x>0,∴1<x<a;
令f′(x)>0,可得x>a或x<1,∵x>0,∴0<x<1或x>a
∴函數f(x)在(0,1),(a,+∞)上單調遞增,在(1,a)上單調遞減;
(Ⅱ)a=-1時,f(x)=-lnx+$\frac{{x}^{x}}{2}$,(x>0),
f′(x)=$\frac{(x+1)(x-1)}{x}$,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)遞減,在(1,+∞)遞增,
∴x=1時,f(x)取最小值是f(1)=$\frac{1}{2}$,
故f(x)≥$\frac{1}{2}$成立.
點評 本題考查函數的單調性,考查導數知識的運用,考查分類討論的數學思想,屬于中檔題.


科目:高中數學 來源: 題型:解答題
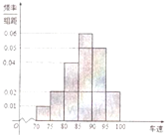 我州某高中一研究性學習小組,在某一告訴公路服務區進行社會實踐活動,從小型汽車中按進服務區的先后,每間隔5輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100),統計后得到如圖的頻率分布直方圖.
我州某高中一研究性學習小組,在某一告訴公路服務區進行社會實踐活動,從小型汽車中按進服務區的先后,每間隔5輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100),統計后得到如圖的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
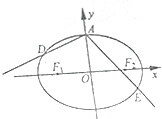 如圖,橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,長軸長為2$\sqrt{2}$,左、右焦點分別為F1,F2,上頂點為A.
如圖,橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,長軸長為2$\sqrt{2}$,左、右焦點分別為F1,F2,上頂點為A.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com