
分析 (Ⅰ)利用離心率和a,b與c的關系求得a和b的關系,根據橢圓的幾何性質知,當點P為橢圓的短軸端點時,△PF1F2的面積最大,進而求得bc的關系,最后聯立求得a和b,則橢圓的方程可得.
(Ⅱ)先對直線l的斜率分類討論,當直線l的斜率不存在時,求出的值;當直線l的斜率存在時,設l:y=k(x+1),聯立l與橢圓的方程,消去y得到關于x的一元二次方程,再結合根系數的關系利用向量的數量積坐標公式即可求得$\overrightarrow{{F_2}M}$•$\overrightarrow{{F_2}N}$的取值范圍,從而解決問題.
解答 解:(Ⅰ)由題知$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{1}{2}•2c•b=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=$\sqrt{2}$,b=1,c=1,即橢圓方程為$\frac{x^2}{2}+{y^2}=1$,
(Ⅱ)當直線MN的斜率不存在時,則MN的方程為x=1,此時M(1,$\frac{\sqrt{2}}{2}$),(1,-$\frac{\sqrt{2}}{2}$),$\overrightarrow{{F_2}M}$•$\overrightarrow{{F_2}N}$=-$\frac{1}{2}$
當直線MN的斜率存在時,設MN的方程為:y=k(x-1),聯立得到方程組
$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,消去y得(2k2+1)x2-4k2x+2k2-2=0,
設M(x1,y1),N(x2,y2),
則x1+x2=$\frac{4{k}^{2}}{2{k}^{2}+1}$,x1x2=$\frac{2{k}^{2}-2}{2{k}^{2}+1}$,
∴$\overrightarrow{{F_2}M}$•$\overrightarrow{{F_2}N}$=(x1-1,y1)•(x2-1,y2)=(1+k2)[x1x2-(x1+x2)+1]=-$\frac{1}{2-\frac{1}{1+{k}^{2}}}$
∵k2≥0,
∴0<$\frac{1}{1+{k}^{2}}$≤1,
∴1≤2-<$\frac{1}{1+{k}^{2}}$≤2,
∴-1≤$\overrightarrow{{F_2}M}$•$\overrightarrow{{F_2}N}$<-$\frac{1}{2}$,
∴$\overrightarrow{{F_2}M}$•$\overrightarrow{{F_2}N}$的取值范圍為[-1,-$\frac{1}{2}$)
點評 本題考查的知識點是直線與圓的位置關系,直線與圓錐曲線的綜合應用,其中根據已知條件求出橢圓的標準方程是解答本題的關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | (1,+∞) | B. | (2,4) | C. | (-∞,-1)∪(1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -144 | B. | -36 | C. | -57 | D. | 34 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-4)∪(4,+∞) | B. | (-∞,-4)∪(-2,0)∪(2,4) | C. | (-∞,-4)∪(-2,0) | D. | (-4,-2)∪(2,4) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖在平行四邊形ABCD中,O是AC與BD的交點,P、Q、M、N分別是線段OA、OB、OC、OD的中點.在A、P、M、C中任取一點記為E,在B、Q、N、D中任取一點記為F.設G為滿足向量$\overrightarrow{OG}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$的點,則在上述的點G組成的集合中的點,落在平行四邊形ABCD外(不含邊界)的概率為( )
如圖在平行四邊形ABCD中,O是AC與BD的交點,P、Q、M、N分別是線段OA、OB、OC、OD的中點.在A、P、M、C中任取一點記為E,在B、Q、N、D中任取一點記為F.設G為滿足向量$\overrightarrow{OG}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$的點,則在上述的點G組成的集合中的點,落在平行四邊形ABCD外(不含邊界)的概率為( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 49 | B. | 45 | C. | 69 | D. | 73 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
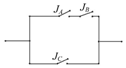 如圖,JA,JB兩個開關串聯再與開關JC并聯,在某段時間內每個開關能夠閉合的概率都是0.5,計算在這段時間內線路正常工作的概率為0.625.
如圖,JA,JB兩個開關串聯再與開關JC并聯,在某段時間內每個開關能夠閉合的概率都是0.5,計算在這段時間內線路正常工作的概率為0.625.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com