
分析 根據$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影是|$\overrightarrow{b}$|×cosθ,列出方程求出m的值,再計算$\overrightarrow{a}$、$\overrightarrow{b}$的夾角θ的值.
解答 解:∵$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影為3,
且|$\overrightarrow{a}$|=$\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}$=2,$\overrightarrow{a}$•$\overrightarrow{b}$=3+$\sqrt{3}$m;
∴|$\overrightarrow{b}$|×cosθ=|$\overrightarrow{b}$|×$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{3+\sqrt{3}m}{2}$=3;
解得m=$\sqrt{3}$,
∴|$\overrightarrow{b}$|=2$\sqrt{3}$;
∴cosθ=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
由θ∈[0,π],
∴$\overrightarrow{a}$、$\overrightarrow{b}$的夾角θ為$\frac{π}{6}$.
故答案為:$\frac{π}{6}$.
點評 本題考查向量在另一個向量上的投影定義及計算公式,向量夾角的應用問題,是基礎題目.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
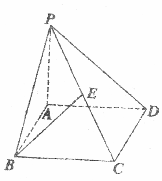 如圖所示,四棱錐P-ABCD的底面是邊長為a的正方形,側棱PA⊥底面ABCD,在側面PBC內,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.
如圖所示,四棱錐P-ABCD的底面是邊長為a的正方形,側棱PA⊥底面ABCD,在側面PBC內,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向右平移$\frac{π}{4}$個單位 | B. | 向左平移$\frac{π}{4}$個單位 | ||
| C. | 向右平移$\frac{π}{12}$個單位 | D. | 向左平移$\frac{π}{12}$個單位 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 2 | C. | 3 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com