Question

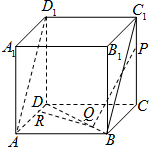
7．如圖，在棱長為1的正方體ABCD-A₁B₁C₁D₁中，P、Q分別是線段CC₁，BD上的點，R是直線AD上的點，滿足PQ∥平面ABC₁D₁，PQ⊥RQ，則|PR|的最小值是（　　）

• A． $\frac{\sqrt{42}}{6}$
• B． $\frac{\sqrt{30}}{5}$
• C． $\frac{\sqrt{5}}{2}$
• D． $\frac{2\sqrt{3}}{3}$

Answer 1

分析 過P作PM∥BC₁，連接MQ并延長MQ交AD于N，則PM∥平面ABC₁D₁，設PC=x，證明△CQM≌△QRN，QR=CQ=$\sqrt{{x}^{2}+（1-x）^{2}}$，CR=$\sqrt{2[{x}^{2}+（1-x）^{2}]}$，即可得出結論．

解答 解：過P作PM∥BC₁，連接MQ并延長MQ交AD于N，
則PM∥平面ABC₁D₁，
∵PQ∥平面ABC₁D₁，PM∩PQ=P，
∴平面PMQ∥平面ABC₁D₁，
∴MQ∥平面ABC₁D₁，
∴MQ∥AB．
設PC=x，則CM=x，QM=BM=1-x，QN=x，CQ=$\sqrt{{x}^{2}+（1-x）^{2}}$．
∵PQ⊥QR，∴CQ⊥RQ，
∴△CQM∽△QRN．
∵QN=CM=x，
∴△CQM≌△QRN，
∴QR=CQ=$\sqrt{{x}^{2}+（1-x）^{2}}$，CR=$\sqrt{2[{x}^{2}+（1-x）^{2}]}$，
PR²=2[x²+（1-x）²]+x²=$5（x-\frac{2}{5}）^{2}+\frac{6}{5}$，
∴$x=\frac{2}{5}$時，PQ取得最小值$\frac{\sqrt{30}}{5}$．
故選B．

點評 本題考查空間距離的計算，考查三角形全等的證明，考查學生分析解決問題的能力，屬于中檔題．