
分析 利用方程組法,兩式相減可求數列{an}的通項公式.
解答 解:數列{an}滿足$\frac{{a}_{1}}{1}$+$\frac{{a}_{2}}{3}$+$\frac{{a}_{3}}{5}$+…+$\frac{{a}_{n}}{2n-1}$=3n+1…①
則有:$\frac{{a}_{1}}{1}$+$\frac{{a}_{2}}{3}$+$\frac{{a}_{3}}{5}$+…+$\frac{{a}_{n-1}}{2(n-1)-1}$=3n…②,
由①-②可得:$\frac{{a}_{n}}{2n-1}$=3n+1-3n=2•3n
∴an=(2n-1)•2•3n
故答案為:(2n-1)•2•3n
點評 本題主要考查數列通項公式的求解,構造了方程組,加減消項法,屬于基礎題.


科目:高中數學 來源: 題型:解答題
| 優秀 | 非優秀 | 總計 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合計 | 105 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{40}{3}$ | B. | $\frac{50}{3}$ | C. | 10 | D. | 20 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
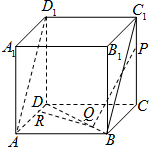 如圖,在棱長為1的正方體ABCD-A1B1C1D1中,P、Q分別是線段CC1,BD上的點,R是直線AD上的點,滿足PQ∥平面ABC1D1,PQ⊥RQ,則|PR|的最小值是( )
如圖,在棱長為1的正方體ABCD-A1B1C1D1中,P、Q分別是線段CC1,BD上的點,R是直線AD上的點,滿足PQ∥平面ABC1D1,PQ⊥RQ,則|PR|的最小值是( )| A. | $\frac{\sqrt{42}}{6}$ | B. | $\frac{\sqrt{30}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在平面直角坐標系xOy中,已知橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,其焦點與橢圓上最近點的距離為2-$\sqrt{2}$.
在平面直角坐標系xOy中,已知橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,其焦點與橢圓上最近點的距離為2-$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com