
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 4 |
| 3 |
(2
|
| 15 |
| 1 |
| 2 |
| 15 |
| 3 |
| 3 |
| 15 |
| 3 |
| 15 |
| 3 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |


 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:高中數學 來源: 題型:
| 1 |
| x |
| ^y |
| ∫ | a 0 |
| π |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
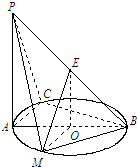 如圖所示,PA⊥平面ABC,點C在以AB為直徑的⊙O上,∠CBA=30°,PA=AB=2,點E為線段PB的中點,點M在弧AB上,且OM∥AC.
如圖所示,PA⊥平面ABC,點C在以AB為直徑的⊙O上,∠CBA=30°,PA=AB=2,點E為線段PB的中點,點M在弧AB上,且OM∥AC.查看答案和解析>>
科目:高中數學 來源: 題型:
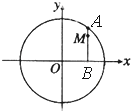 如圖,設A是圓x2+y2=6上的動點,點B是A在x軸上投影,M為AB上一點,且|MB|=
如圖,設A是圓x2+y2=6上的動點,點B是A在x軸上投影,M為AB上一點,且|MB|=
| ||
| 3 |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
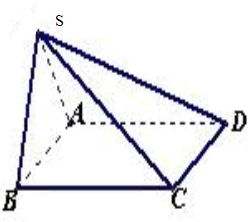
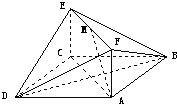 如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
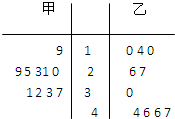 某林管部門在每年植樹節前,為保證樹苗的質量,都會對樹苗進行檢測.現從甲、乙兩種樹苗中各抽取10株,測量其高度,所得數據如莖葉圖所示,則下列描述正確的是( )
某林管部門在每年植樹節前,為保證樹苗的質量,都會對樹苗進行檢測.現從甲、乙兩種樹苗中各抽取10株,測量其高度,所得數據如莖葉圖所示,則下列描述正確的是( )| A、甲樹苗的平均高度大于乙樹苗的平均高度,且甲樹苗比乙樹苗長得整齊 |
| B、甲樹苗的平均高度大于乙樹苗的平均高度,但乙樹苗比甲樹苗長得整齊 |
| C、乙樹苗的平均高度大于甲樹苗的平均高度,但甲樹苗比乙樹苗長得整齊 |
| D、乙樹苗的平均高度大于甲樹苗的平均高度,且乙樹苗比甲樹苗長得整齊 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 5 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com