
| A. | (-2,1) | B. | [-2,1) | C. | [-1,2) | D. | (-1,2) |
分析 由已知中函數的解析式,可判斷出函數f(x)為偶函數,利用導數法分析出函數的單調性,可將不等式f(2x-1)<f(3)化為:|2x-1|<3,解得答案.
解答 解:∵f(x)=e|x|+cosx+|x|,
∴f(-x)=e|-x|+cos(-x)+|-x|=f(x)=e|x|+cosx+|x|=f(x),
故函數f(x)為偶函數,
當x≥0時,f(x)=ex+cosx+x,
f′(x)=ex-sinx+1,
∵f′(x)>0在x≥0時恒成立,
故函數f(x)在[0,+∞)上為增函數,
若f(2x-1)<f(3),則|2x-1|<3,
解得:x∈(-1,2),
故選:D
點評 本題考查的知識點是函數的奇偶性,函數的單調性,利用導數研究函數的單調性,難度中檔.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
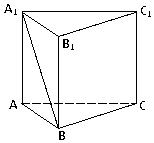 如圖,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;
如圖,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com