
分析 (1)由題意列關于a,b,c的方程組,求解方程組可得a,b的值,則橢圓方程可求;
(2)由題意設出直線l的方程,與橢圓方程聯立,化為關于y的一元二次方程,利用根與系數的關系求得|y1-y2|,代入三角形面積公式,換元后利用基本不等式求得最值.
解答 解.(1)由題意,$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2b=2}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,
故橢圓的標準方程為$\frac{x^2}{4}+{y^2}=1$;
(2)存在△AOB面積的最大值.
∵直線l過點E(-1,0),可設直線l的方程為 x=my-1.
則$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ x=my-1.\end{array}\right.$,整理得(m2+4)y2-2my-3=0.
由△=(2m)2+12(m2+4)>0.
設A(x1,y1),B(x2,y2).
則${y}_{1}+{y}_{2}=\frac{2m}{{m}^{2}+4},{y}_{1}{y}_{2}=\frac{-3}{{m}^{2}+4}$.
∴|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{4\sqrt{{m}^{2}+3}}{{m}^{2}+4}$.
∴${S_{△AOB}}=\frac{1}{2}|{OE}|•|{{y_1}-{y_2}}|$=$\frac{{2\sqrt{{m^2}+3}}}{{{m^2}+4}}=\frac{2}{{\sqrt{{m^2}+3}+\frac{1}{{\sqrt{{m^2}+3}}}}}$.
設$g(t)=t+\frac{1}{t}$,$t=\sqrt{{m^2}+3}$,$t≥\sqrt{3}$.
則g(t)在區間$[\sqrt{3},+∞)$上為增函數,
∴$g(t)≥\frac{{4\sqrt{3}}}{3}$.
∴${S_{△AOB}}≤\frac{{\sqrt{3}}}{2}$,當且僅當m=0時取等號,即${({S_{△AOB}})_{max}}=\frac{{\sqrt{3}}}{2}$.
∴S△AOB的最大值為$\frac{{\sqrt{3}}}{2}$.
點評 本題考查橢圓的簡單性質,考查了直線與橢圓位置關系的應用,體現了“設而不求”的解題思想方法,訓練了利用基本不等式求最值,是中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2,1) | B. | [-2,1) | C. | [-1,2) | D. | (-1,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“若x2=1,則x=1”的否命題為“若x2=1,則x≠1” | |
| B. | 命題“?x≥0,x2+x-1<0”的否定是“?x<0,x2+x-1<0” | |
| C. | “x=-1”是“x2-5x-6=0”的必要不充分條件 | |
| D. | 命題“若x=y,則sinx=siny”的逆否命題為真命題. |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
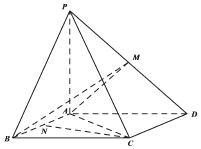 如圖,四棱錐P-ABCD中,底面ABCD為平行四邊形,PA⊥底面ABCD,M是棱PD的中點,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如圖,四棱錐P-ABCD中,底面ABCD為平行四邊形,PA⊥底面ABCD,M是棱PD的中點,且PA=AB=AC=2,BC=2$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | -7 | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com