
【題目】已知函數f(x)的定義域是(0,+∞),且滿足f(xy)=f(x)+f(y),當x>1時,有f(x)>0.
(1)求f(1),判定并證明f(x)的單調性;
(2)若f(2)=1,解不等式f(﹣x)+f(3﹣x)≥﹣2.
【答案】
(1)解:令x=y=1,則f(1)=f(1)+f(1),解得f(1)=0.
f(x)在(0,+∞)上的是增函數,
設x1,x2∈(0,+∞),且x1>x2,則 ![]() >1,
>1,
∴f( ![]() )>0,
)>0,
∴f(x1)﹣f(x2)=f(x2 ![]() )﹣f(x2)=f(
)﹣f(x2)=f( ![]() )>0,
)>0,
即f(x1)>f(x2),
∴f(x)在(0,+∞)上的是增函數
(2)解:∵f(2)=1,∴f(﹣x)+f(3﹣x)≥﹣2,
可化為f(﹣x)+f(3﹣x)≥﹣2f(2).
∴f(﹣x)+f(2)+f(3﹣x)+f(2)≥0,
∴f(﹣2x)+f(6﹣2x)≥f(1),
∴f[﹣2x(6﹣2x)]≥f(1),
∴ 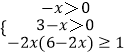 ,
,
∴x≤ ![]() .
.
∴不等式的解集為{x|x≤ ![]() }
}
【解析】(1)利用賦值法進行求f(1)的值; 根據函數的單調性的定義判斷f(x)在(0,+∞)上的單調性,并證明.(2)根據函數單調性的性質解不等式即可.
【考點精析】本題主要考查了函數單調性的判斷方法的相關知識點,需要掌握單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】選修4![]() 4:坐標系與參數方程
4:坐標系與參數方程
在直角坐標系![]() 中,已知直線l1:
中,已知直線l1: ![]() (
(![]() ,
, ![]() ),拋物線C:
),拋物線C: 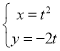 (t為參數).以原點
(t為參數).以原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(Ⅰ)求直線l1 和拋物線C的極坐標方程;
(Ⅱ)若直線l1 和拋物線C相交于點A(異于原點O),過原點作與l1垂直的直線l2,l2和拋物線C相交于點B(異于原點O),求△OAB的面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年某市街頭開始興起“mobike”、“ofo”等共享單車,這樣的共享單車為很多市民解決了最后一公里的出行難題.然而,這種模式也遇到了一些讓人尷尬的問題,比如亂停亂放,或將共享單車占為“私有”等.為此,某機構就是否支持發展共享單車隨機調查了50人,他們年齡的分布及支持發展共享單車的人數統計如下表:
年齡 |
|
|
|
|
|
|
受訪人數 | 5 | 6 | 15 | 9 | 10 | 5 |
支持發展共享單車人數 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上統計數據填寫下面的![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.1的前提下,認為年齡與是否支持發展共享單車有關系:
列聯表,并判斷能否在犯錯誤的概率不超過0.1的前提下,認為年齡與是否支持發展共享單車有關系:
年齡低于35歲 | 年齡不低于35歲 | 合計 | |
支持 | |||
不支持 | |||
合計 |
(Ⅱ)若對年齡在![]() 的被調查人中隨機選取兩人,對年齡在
的被調查人中隨機選取兩人,對年齡在![]() 的被調查人中隨機選取一人進行調查,求選中的3人中支持發展共享單車的人數為2人的概率.
的被調查人中隨機選取一人進行調查,求選中的3人中支持發展共享單車的人數為2人的概率.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式: 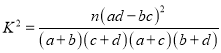 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠每日生產一種大型產品1件,每件產品的投入成本為2000元.產品質量為一等品的概率為![]() ,二等品的概率為
,二等品的概率為![]() ,每件一等品的出廠價為10000元,每件二等品的出廠價為8000元.若產品質量不能達到一等品或二等品,除成本不能收回外,沒生產一件產品還會帶來1000元的損失.
,每件一等品的出廠價為10000元,每件二等品的出廠價為8000元.若產品質量不能達到一等品或二等品,除成本不能收回外,沒生產一件產品還會帶來1000元的損失.
(1)求在連續生產3天中,恰有一天生產的兩件產品都為一等品的的概率;
(2)已知該廠某日生產的2件產品中有一件為一等品,求另一件也為一等品的概率;
(3)求該廠每日生產該種產品所獲得的利潤![]() (元)的分布列及數學期望.
(元)的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
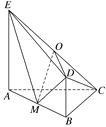
【題目】如圖所示,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四邊形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=![]() AE=2,O,M分別為CE,AB的中點.
AE=2,O,M分別為CE,AB的中點.
(1)求證:OD∥平面ABC;
(2)求直線CD和平面ODM所成角的正弦值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某大學聯盟的自主招生考試中,報考文史專業的考生參加了人文基礎學科考試科目“語文”和“數學”的考試.某考場考生的兩科考試成績數據統計如下圖所示,本次考試中成績在![]() 內的記為
內的記為![]() ,其中“語文”科目成績在
,其中“語文”科目成績在![]() 內的考生有10人.
內的考生有10人.
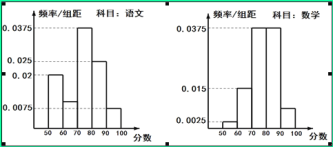
(1)求該考場考生數學科目成績為![]() 的人數;
的人數;
(2)已知參加本考場測試的考生中,恰有2人的兩科成績均為![]() .在至少一科成績為
.在至少一科成績為![]() 的考生中,隨機抽取2人進行訪談,求這2人的兩科成績均為
的考生中,隨機抽取2人進行訪談,求這2人的兩科成績均為![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列給出四組函數,表示同一函數的是( )
A.f(x)=x﹣1,g(x)= ![]() ﹣1
﹣1
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=|x|,g(x)= ![]()
D.f(x)=1,g(x)=x0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() (a,b為常數)是定義在(﹣1,1)上的奇函數,且f(
(a,b為常數)是定義在(﹣1,1)上的奇函數,且f( ![]() )=
)= ![]()
(1)求函數f(x)的解析式;
(2)用定義證明f(x)在(﹣1,1)上是增函數并求值域;
(3)求不等式f(2t﹣1)+f(t)<0的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com