【題目】在某大學聯盟的自主招生考試中，報考文史專業的考生參加了人文基礎學科考試科目“語文”和“數學”的考試.某考場考生的兩科考試成績數據統計如下圖所示，本次考試中成績在
內的記為
，其中“語文”科目成績在
內的考生有10人.
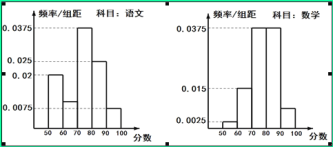
（1）求該考場考生數學科目成績為的人數；
（2）已知參加本考場測試的考生中，恰有2人的兩科成績均為.在至少一科成績為的考生中，隨機抽取2人進行訪談，求這2人的兩科成績均為的概率.
【答案】(1)3;(2)
.
【解析】
試題分析：(1)頻率分布直方圖中面積表示頻率，設頻率=
,
為總人數，所以
，結合
的頻率，
；
(2)首先算出語文與數學中成績為
的人數，通過列舉的方法計算出選出的2人所有可能的情況及這兩人的兩科成績等級均為
的情況；利用古典概型概率公式求出隨機抽取兩人進行訪談，這兩人的兩科成績等級均為的概率。
試題解析：（1）該考場的考生人數為10÷0.25=40人. 2分
數學科目成績為
的人數為
40×(1-0.0025×10-0.015×10-0.0375×10×2)=40×0.075=3人. 6分
（2）語文和數學成績為A的各有3人，其中有兩人的兩科成績均為，所以還有兩名同學只有一科成績為. 8分
設這四人為甲、乙、丙、丁，其中甲、乙的兩科成績均為，則在至少一科成績為的考生中，隨機抽取兩人進行訪談，基本事件為{甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}， {丙，丁}共6個， 10分
設“隨機抽取兩人，這兩人的兩科成績均為”為事件
，則事件包含的事件有1個，則
. 12分
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知圓
的圓心在直線
上，且與直線
相切于點
，
（1）求圓
方程；
（2）是否存在過點
的直線
與圓
交于
兩點，且
的面積是
（
為坐標原點），若存在，求出直線
的方程，若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）的定義域是（0，+∞），且滿足f（xy）=f（x）+f（y），當x＞1時，有f（x）＞0．
（1）求f（1），判定并證明f（x）的單調性；
（2）若f（2）=1，解不等式f（﹣x）+f（3﹣x）≥﹣2．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校上學期的期中考試后，為了了解某學科的考試成績，根據學生的考試成績利用分層抽樣抽取
名學生的成績進行統計（所有學生成績均不低于
分），得到學生成績的頻率分布直方圖如圖，回答下列問題；
（Ⅰ）根據頻率分布直方圖計算本次考試成績的平均分；
（Ⅱ）已知本次全校考試成績在
內的人數為
，試確定全校的總人數；
（Ⅲ）若本次考試抽查的
人中考試成績在
內的有
名女生，其余為男生，從中選擇兩名學生，求選擇一名男生與一名女生的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=ax2+bx+1，a，b∈R，當x=﹣1時，函數f（x）取到最小值，且最小值為0；
（1）求f（x）解析式；
（2）關于x的方程f（x）=|x+1|﹣k+3恰有兩個不相等的實數解，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】運貨卡車以每小時x千米的速度勻速行駛130千米，按交通法規限制50≤x≤100（單位：千米/時）．假設汽油的價格是每升2元，而汽車每小時耗油
升，司機的工資是每小時14元．
（1）求這次行車總費用y關于x的表達式；
（2）當x為何值時，這次行車的總費用最低，并求出最低費用的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某校高三學生的視力情況，隨機地抽查了該校100名高三學生的視力情況，得到頻率分布直方圖如下圖，由于不慎將部分數據丟失，但知道前4組的頻數成等比數列，后6組的頻數成等差數列，設最大頻率為a，視力在4.6到5.0之間的學生數為b，則a，b的值分別為 ( )
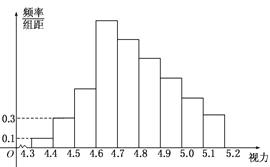
A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
