
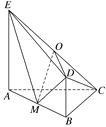
【題目】如圖所示,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四邊形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=![]() AE=2,O,M分別為CE,AB的中點(diǎn).
AE=2,O,M分別為CE,AB的中點(diǎn).
(1)求證:OD∥平面ABC;
(2)求直線CD和平面ODM所成角的正弦值;
【答案】(1)見解析(2)![]()
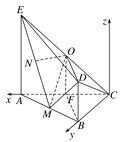
【解析】試題分析:(1)通過證明線線平行得到線面平行;(2)C為原點(diǎn),分別以CA,CB所在直線為x,y軸,以過點(diǎn)C且與平面ABC垂直的直線為z軸,建立空間直角坐標(biāo)系,求出平面ODM的一個法向量,利用直線與平面所成的角的公式,求出直線CD和平面ODM所成角的正弦值。
試題解析:(1)證明 如圖,取AC中點(diǎn)F,連接OF,FB.
∵F是AC中點(diǎn),O為CE中點(diǎn),
∴OF∥EA且OF=![]() EA.
EA.
又BD∥AE且BD=![]() AE,
AE,
∴OF∥DB且OF=DB,
∴四邊形BDOF是平行四邊形,∴OD∥FB.
又∵FB平面ABC,OD平面ABC,
∴OD∥平面ABC.
(2)解 ∵平面ABDE⊥平面ABC,平面ABDE∩平面ABC=AB,DB平面ABDE,且BD⊥BA,
∴DB⊥平面ABC.
∵BD∥AE,∴EA⊥平面ABC.
又△ABC是等腰直角三角形,且AC=BC,
∴∠ACB=90°,
∴以C為原點(diǎn),分別以CA,CB所在直線為x,y軸,以過點(diǎn)C且與平面ABC垂直的直線為z軸,建立空間直角坐標(biāo)系,如圖所示.
∵AC=BC=4,∴C(0,0,0),A(4,0,0),B(0,4,0),D(0,4,2),E(4,0,4),O(2,0,2),M(2,2,0),
∴![]() =(0,4,2),
=(0,4,2),![]() =(-2,4,0),
=(-2,4,0),![]() =(-2,2,2).
=(-2,2,2).
設(shè)平面ODM的法向量為n=(x,y,z),
則由n⊥![]() ,n⊥
,n⊥![]() ,可得
,可得![]()
令x=2,得y=1,z=1,∴n=(2,1,1).
設(shè)直線CD和平面ODM所成角為θ,
則sin θ=![]() =
=![]() =
=![]() =
=![]() .
.
∴直線CD和平面ODM所成角的正弦值為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知下圖中,四邊形 ABCD是等腰梯形, ![]() ,
, ![]() ,O、Q分別為線段AB、CD的中點(diǎn),OQ與EF的交點(diǎn)為P,OP=1,PQ=2,現(xiàn)將梯形ABCD沿EF折起,使得
,O、Q分別為線段AB、CD的中點(diǎn),OQ與EF的交點(diǎn)為P,OP=1,PQ=2,現(xiàn)將梯形ABCD沿EF折起,使得![]() ,連結(jié)AD、BC,得一幾何體如圖所示.
,連結(jié)AD、BC,得一幾何體如圖所示.
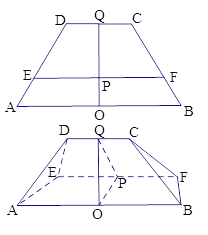
(Ⅰ)證明:平面ABCD![]() 平面ABFE;
平面ABFE;
(Ⅱ)若上圖中, ![]() ,CD=2,求平面ADE與平面BCF所成銳二面角的余弦值.
,CD=2,求平面ADE與平面BCF所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若存在唯一整數(shù)![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)=lgx+1(1≤x≤100),則g(x)=f2(x)+f(x2)的值域?yàn)椋?/span> )
A.[﹣2,7]
B.[2,7]
C.[﹣2,14]
D.[2,14]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)的定義域是(0,+∞),且滿足f(xy)=f(x)+f(y),當(dāng)x>1時,有f(x)>0.
(1)求f(1),判定并證明f(x)的單調(diào)性;
(2)若f(2)=1,解不等式f(﹣x)+f(3﹣x)≥﹣2.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,內(nèi)角A,B,C的對邊分別為a,b,c,且(2b-c)cos A=acos C.
(1)求角A的大小;
(2)若a=3,b=2c,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)f(x)=ax2+bx+1,a,b∈R,當(dāng)x=﹣1時,函數(shù)f(x)取到最小值,且最小值為0;
(1)求f(x)解析式;
(2)關(guān)于x的方程f(x)=|x+1|﹣k+3恰有兩個不相等的實(shí)數(shù)解,求實(shí)數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩家商場對同一種商品開展促銷活動,對購買該商品的顧客兩家商場的獎勵方案如下:
甲商場:顧客轉(zhuǎn)動如圖所示圓盤,當(dāng)指針指向陰影部分(圖中四個陰影部分均為扇形,且每個扇形圓心角均為15°,邊界忽略不計) 即為中獎.

乙商場:從裝有3個白球3個紅球的盒子中一次性摸出2個球(球除顏色外不加區(qū)分),如果摸到的是2個紅球,即為中獎.
問:購買該商品的顧客在哪家商場中獎的可能性大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點(diǎn)
,且過點(diǎn)![]() .
.
(Ⅰ)求橢圓![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是橢圓
是橢圓![]() 上兩個不同的動點(diǎn),且使
上兩個不同的動點(diǎn),且使![]() 的角平分線垂直于
的角平分線垂直于![]() 軸,試判斷直線
軸,試判斷直線![]() 的斜率是否為定值?若是,求出該值;若不是,說明理由.
的斜率是否為定值?若是,求出該值;若不是,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com