
分析 (1)設|F1P|=m,|F2P|=n,$\overrightarrow{{F}_{1}M}$=-2$\overrightarrow{M{F}_{2}}$,可得F2是線段F1M的中點,又線段NF1的中點P在橢圓上,△F1MN周長為12.可得m+n=2a,2m+2n+4c=12,可得a+c=3.由橢圓的離心率e=$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,解出即可得出.
(2)如圖所示,①當AB⊥x軸時,把x=±1代入橢圓方程可得:$\frac{1}{4}+\frac{{y}^{2}}{3}$=1,解出可得:$\overrightarrow{OA}$$•\overrightarrow{OB}$=-$\frac{5}{4}$.
②當AB的斜率存在時,設切線AB的方程為:y=kx+m.利用切線的性質可得$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,即:m2=1+k2.設A(x1,y1),B(x2,y2).把y=kx+m代入橢圓方程可得:(3+4k2)x2+8kmx+4m2-12=0,把根與系數的關系代入$\overrightarrow{OA}$$•\overrightarrow{OB}$=x1x2+y1y2=$-\frac{5+5{k}^{2}}{3+4{k}^{2}}$,即可得出.
解答 解:(1)設|F1P|=m,|F2P|=n,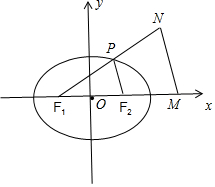
∵$\overrightarrow{{F}_{1}M}$=-2$\overrightarrow{M{F}_{2}}$,∴F2是線段F1M的中點,
又線段NF1的中點P在橢圓上,△F1MN周長為12.
∴m+n=2a,2m+2n+4c=12,可得a+c=3.
由橢圓的離心率e=$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,
解得a=2,c=1,b2=3.
∴橢圓C的方程為:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)如圖所示,
①當AB⊥x軸時,把x=±1代入橢圓方程可得:$\frac{1}{4}+\frac{{y}^{2}}{3}$=1,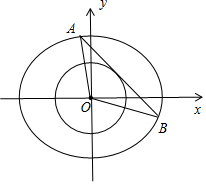
解得:y=$±\frac{3}{2}$.
可得:$\overrightarrow{OA}$$•\overrightarrow{OB}$=$1-\frac{9}{4}$=-$\frac{5}{4}$.
②當AB的斜率存在時,設切線AB的方程為:y=kx+m.
則$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,化為:m2=1+k2.
設A(x1,y1),B(x2,y2).
把y=kx+m代入橢圓方程可得:(3+4k2)x2+8kmx+4m2-12=0,
△>0.
∴x1+x2=$\frac{-8km}{3+4{k}^{2}}$,x1•x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
∴y1y2=(kx1+m)(kx2+m)=km(x1+x2)+k2x1•x2+m2
∴$\overrightarrow{OA}$$•\overrightarrow{OB}$=x1x2+y1y2=km(x1+x2)+(k2+1)x1•x2+m2
=km•$\frac{-8km}{3+4{k}^{2}}$+(k2+1)$\frac{4{m}^{2}-12}{3+4{k}^{2}}$+m2
=$\frac{7{m}^{2}-12{k}^{2}-12}{3+4{k}^{2}}$
=$-\frac{5+5{k}^{2}}{3+4{k}^{2}}$
=$-\frac{5}{4}$-$\frac{5}{12+16{k}^{2}}$∈$[-\frac{5}{3},-\frac{5}{4})$,
綜上可得:$\overrightarrow{OA}$$•\overrightarrow{OB}$∈$[-\frac{5}{3},-\frac{5}{4}]$.
點評 本題考查了直線與橢圓相交問題、一元二次方程的根與系數的關系、直線與圓相切的性質、點到直線的距離公式、數量積運算性質、函數的性質,考查了推理能力與計算能力,屬于難題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
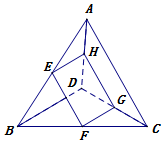 如圖,E,F,G,H分別是空間四邊形ABCD的邊AB,BC,CD,DA上的中點.
如圖,E,F,G,H分別是空間四邊形ABCD的邊AB,BC,CD,DA上的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)+x<m+n | B. | f(x)+x>m+n | C. | f(x)-x<0 | D. | f(x)-x>0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 看營養說明 | 不看營養說明 | 合計 | |
| 男大學生 | 26 | 6 | 32 |
| 女大學生 | 14 | 18 | 32 |
| 合計 | 40 | 24 | 64 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com