
| A. | 若a,b,c∈R,則“ax2+bx+c≥0”的充分條件是“b2-4ac≤0” | |
| B. | 若a,b,c∈R,則“ab2>cb2”的充要條件是“a>c” | |
| C. | l是一條直線,α,β是兩個不同的平面,若l⊥α,l⊥β,則α∥β | |
| D. | 命題“對任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0” |
分析 A.根據充分條件的定義進行判斷,
B.根據充要條件的定義進行判斷,
C.根據線面垂直和面面平行的性質進行判斷,
D.根據全稱命題的否定是特稱命題進行判斷.
解答 解:A.當a>0,b=0,c≥0時,滿足b2-4ac≤0,但ax2+bx+c≥0不恒成立,故A錯誤,
B.當b=0,a>c時,ab2>cb2不成立,即必要性不成立,故B錯誤,
C.根據線面垂直的性質得若l⊥α,l⊥β,則α∥β成立,故C正確,
D.命題“對任意x∈R,有x2≥0”的否定是“存在x∈R,有x2<0”,故D錯誤,
故選:C
點評 本題主要考查命題的真假平時,涉及充分條件和必要條件的判斷,空間線面平行的位置關系以及含有量詞的命題的否定,涉及的知識點較多,難度不大.


科目:高中數學 來源: 題型:選擇題
| A. | $(-\frac{5π}{12},\frac{π}{12})$ | B. | $(-\frac{π}{6},\frac{π}{3})$ | C. | $(-\frac{π}{12},\frac{5π}{12})$ | D. | $(\frac{π}{12},\frac{7π}{12})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 2 | C. | 4 | D. | 4034 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
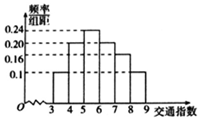 隨著社會發展,廣州市在一天的上下班時段經常會出現堵車嚴重的現象.交通指數是交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念.記交通指數為T,其范圍為[0,10],分別有5個級別;T∈[0,2)暢通;T∈[2,4)基本暢通;T∈[4,6)輕度擁堵;T∈[6,8)中度擁堵;T∈[8,10)嚴重擁堵.早高峰時段(T≥3),從廣州市交通指揮中心隨機選取了50個交通路段進行調查,依據交通指數數據繪制的直方圖如圖所示:
隨著社會發展,廣州市在一天的上下班時段經常會出現堵車嚴重的現象.交通指數是交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念.記交通指數為T,其范圍為[0,10],分別有5個級別;T∈[0,2)暢通;T∈[2,4)基本暢通;T∈[4,6)輕度擁堵;T∈[6,8)中度擁堵;T∈[8,10)嚴重擁堵.早高峰時段(T≥3),從廣州市交通指揮中心隨機選取了50個交通路段進行調查,依據交通指數數據繪制的直方圖如圖所示:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com