
分析 解出f(x)在[a,+∞)上的零點,對f(x)在各段上零點個數進行討論,得出a的值.
解答 解:f(x)=$\left\{\begin{array}{l}{2a-x-\frac{4}{x}-3,x∈(-∞,a)}\\{x-\frac{4}{x}-3,x∈[a,+∞)}\end{array}\right.$,
令x-$\frac{4}{x}$-3=0,解得x=-1或x=4.
(1)若a≤-1,則x2=-1,x3=4,
∵2x2=x1+x3,∴x1=-6,
∴x1=-6是方程-x-$\frac{4}{x}$+2a-3=0的解,
∴6+$\frac{2}{3}$+2a-3=0,解得a=-$\frac{11}{6}$.
(2)若-1<a≤4,則x3=4,∴x2=$\frac{{x}_{1}+4}{2}$,且x1,x2為方程-x-$\frac{4}{x}$+2a-3=0的解,
即x1,x2為x2+(3-2a)x+4=0,
∴x1+x2=2a-3,x1x2=4,
解得x1=-2-2$\sqrt{3}$,x2=1-$\sqrt{3}$或x1=-2+2$\sqrt{3}$,x2=1+$\sqrt{3}$.
若x1=-2-2$\sqrt{3}$,x2=1-$\sqrt{3}$,則a=$\frac{{x}_{1}+{x}_{2}+3}{2}$=$\frac{-1-3\sqrt{3}}{2}$,與a>-1矛盾,
若x1=-2+2$\sqrt{3}$,x2=1+$\sqrt{3}$,則a=$\frac{{x}_{1}+{x}_{2}+3}{2}$=$\frac{-1+3\sqrt{3}}{2}$,與x2<a矛盾.
(3)若a>4,則f(x)在[a,+∞)上無零點,而f(x)=0在(-∞,a)上最多只有兩解,與f(x)有三個零點矛盾.
綜上,a=-$\frac{11}{6}$.
故答案為:-$\frac{11}{6}$
點評 本題考查了分段函數的零點計算,一元二次方程的解法,分類討論思想,屬于中檔題


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{65}{9}$,25] | B. | [$\frac{36}{5}$,25] | C. | [16,25] | D. | [9,25] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
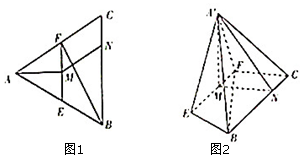 如圖,已知等邊△ABC中,E,F分別為AB,AC邊的中點,M為EF的中點,N為BC邊上一點,且CN=$\frac{1}{4}$BC,將△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.
如圖,已知等邊△ABC中,E,F分別為AB,AC邊的中點,M為EF的中點,N為BC邊上一點,且CN=$\frac{1}{4}$BC,將△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com