【題目】劉徽是我國古代偉大的數學家，他的杰作《九章算術注》和《海島算經》是我國最寶貴的數學遺產劉徽是世界上最早提出十進小數概念的人，他正確地提出了正負數的概念及其加減運算的規則．提出了“割圓術”，并用“割圓術”求出圓周率π為3.14．劉徽在割圓術中提出的“割之彌細，所失彌少，割之又割以至于不可割，則與圓合體而無所失矣”被視為中國古代極限觀念的佳作．其中“割圓術”的第一步是求圓的內接正六邊形的面積，第二步是求圓的內接正十二邊形的面積，依此類推．若在圓內隨機取一點，則該點取自該圓內接正十二邊形的概率為（ ）
A.
B.
C.
D.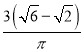
科目：高中數學 來源： 題型：
【題目】設橢圓
的右頂點為A，上頂點為B．已知橢圓的離心率為
，
．
（1）求橢圓的方程；
（2）設直線
與橢圓交于
，
兩點，
與直線
交于點M，且點P，M均在第四象限．若
的面積是
面積的2倍，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（多選題）下列說法正確的是（ ）
A.在回歸直線方程
中，當解釋變量
每增加1個單位時，預報變量
平均減少2.3個單位
B.兩個具有線性相關關系的變量，當相關指數
的值越接近于0，則這兩個變量的相關性就越強
C.若兩個變量的相關指數
，則說明預報變量的差異有88%是由解釋變量引起的
D.在回歸直線方程中，相對于樣本點
的殘差為
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點F1為橢圓
的左焦點，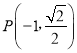
在橢圓上，PF1⊥x軸．
（1）求橢圓的方程：
（2）已知直線l與橢圓交于A，B兩點，且坐標原點O到直線l的距離為
的大小是否為定值？若是，求出該定值：若不是，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位年會進行抽獎活動，在抽獎箱里裝有
張印有“一等獎”的卡片， 
張印
有“二等獎”的卡片， 3張印有“新年快樂”的卡片，抽中“一等獎”獲獎
元， 抽中“二等獎”獲獎
元，抽中“新年快樂”無獎金.
（1）單位員工小張參加抽獎活動，每次隨機抽取一張卡片，抽取后不放回.假如小張一定要將所有獲獎卡片全部抽完才停止. 記
表示“小張恰好抽獎
次停止活動”，求
的值；
（2）若單位員工小王參加抽獎活動，一次隨機抽取
張卡片.
①
記
表示“小王參加抽獎活動中獎”，求
的值；
②設
表示“小王參加抽獎活動所獲獎金數（單位：元）”，求
的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設拋物線
的焦點為
，準線為
，
為過焦點且垂直于
軸的拋物線
的弦，已知以為直徑的圓經過點
.
（1）求
的值及該圓的方程；
（2）設
為上任意一點，過點作的切線，切點為
，證明：
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
