
分析 (1)利用兩個向量的數量積的定義,兩個向量的數量積公式,求得$\overrightarrow{a}$+$\overrightarrow{b}$與$\overrightarrow{a}$-$\overrightarrow{b}$的夾角θ的余弦值,可得求$\overrightarrow{a}$+$\overrightarrow{b}$與$\overrightarrow{a}$-$\overrightarrow{b}$的夾角θ.
(2)根據兩個向量垂直的性質,求得實數λ的值.
解答 解:(1)由題意可得$\overrightarrow{a}$+$\overrightarrow{b}$=(-1,2),得$\overrightarrow{a}$-$\overrightarrow{b}$=(3,4),
∴cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}|•|\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{-3+8}{\sqrt{5}•5}$=$\frac{{\sqrt{5}}}{5}$.
(2)由題意根據若$\overrightarrow{a}$•($\overrightarrow{a}$+λ$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$+λ•$\overrightarrow{a}•\overrightarrow{b}$=10+λ•(-2-3)=0,∴λ=2.
點評 本題主要考查兩個向量的數量積的定義,兩個向量的數量積公式的應用,兩個向量垂直的性質,屬于基礎題.


 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
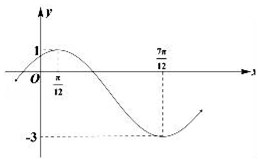 已知函數f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示:
已知函數f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 2 或-1 | C. | -2或1 | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com