
分析 (1)通過x與-4以及2的大小比較,去掉絕對值符號,化簡不等式,然后求解即可.
(2)利用絕對值的幾何意義,求出函數的最小值,然后化簡不等式求解a的范圍即可.
解答 解:(1)函數f(x)=|x-2|+|x+4|,g(x)=x2+4x+3,
不等式f(x)≥g(x)即:|x-2|+|x+4|≥x2+4x+3,
①當x<-4時,不等式化為:-(x-2)-(x+4)≥x2+4x+3,
解得:-5≤x≤-1,∴-5≤x<-4;
②當-4≤x≤2時,不等式化為:-(x-2)+(x+4)≥x2+4x+3,
解得:-2-$\sqrt{7}$≤x≤-2+$\sqrt{7}$,
∴-4≤x$≤-2+\sqrt{7}$;
③當x>2時,不等式化為:(x-2)+(x+4)≥x2+4x+3,
解得:x∈∅,
綜上:不等式的解集為:{x|-5≤x$≤-2+\sqrt{7}$};
(2)因為|x-2|+|x+4|≥|x-2-x-4|=6,
f(x)≥|1-5a|恒成立,
所以6≥|1-5a|,即-6≤1-5a≤6,解得-1$≤a≤\frac{7}{5}$,
所以實數a的取值范圍[-1,$\frac{7}{5}$].
點評 本題考查函數恒成立,不等式的解法,考查化簡以及計算能力.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
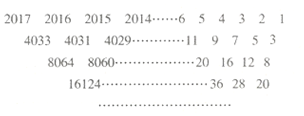 “楊輝三角”又稱“賈憲三角”,是因為賈憲約在公元1050年首先使用“賈憲三角”進行高次開方運算,而楊輝在公元1261年所著的《詳解九章算法》一書中,輯錄了賈憲三角形數表,并稱之為“開方作法本源”圖.下列數表的構造思路就源于“楊輝三角”.該表由若干行數字組成,從第二行起,每一行中的數字均等于其“肩上”兩數之和,表中最后一行僅有一個數,則這個數是( )
“楊輝三角”又稱“賈憲三角”,是因為賈憲約在公元1050年首先使用“賈憲三角”進行高次開方運算,而楊輝在公元1261年所著的《詳解九章算法》一書中,輯錄了賈憲三角形數表,并稱之為“開方作法本源”圖.下列數表的構造思路就源于“楊輝三角”.該表由若干行數字組成,從第二行起,每一行中的數字均等于其“肩上”兩數之和,表中最后一行僅有一個數,則這個數是( )| A. | 2017×22016 | B. | 2018×22015 | C. | 2017×22015 | D. | 2018×22016 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,4] | B. | (2,4] | C. | (3,4) | D. | {3,4} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com