
對于數列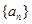 ,把
,把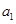 作為新數列
作為新數列 的第一項,把
的第一項,把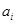 或
或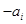 (
(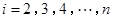 )作為新數列
)作為新數列 的第
的第 項,數列
項,數列 稱為數列
稱為數列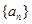 的一個生成數列.例如,數列
的一個生成數列.例如,數列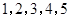 的一個生成數列是
的一個生成數列是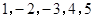 .已知數列
.已知數列 為數列
為數列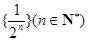 的生成數列,
的生成數列,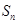 為數列
為數列 的前
的前 項和.
項和.
(1)寫出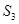 的所有可能值;
的所有可能值;
(2)若生成數列 滿足
滿足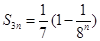 ,求數列
,求數列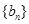 的通項公式;
的通項公式;
(3)證明:對于給定的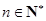 ,
,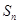 的所有可能值組成的集合為
的所有可能值組成的集合為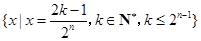 .
.
(1) (2)
(2)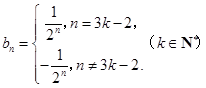 (3)詳見解析.
(3)詳見解析.
解析試題分析:(1)列舉出數列 所有可能情況,共
所有可能情況,共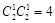 種,分別計算和值為
種,分別計算和值為 ,本題目的初步感觀生成數列
,本題目的初步感觀生成數列 (2)已知和項解析式,則可利用
(2)已知和項解析式,則可利用 求通項. 當
求通項. 當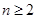 時,
時,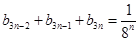 ,而
,而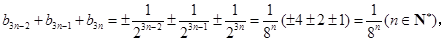 當且僅當
當且僅當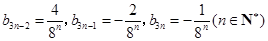 時,才成立.所以
時,才成立.所以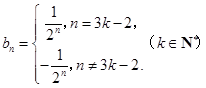 (3)本題實際是對(1)的推廣.證明的實質是確定集合
(3)本題實際是對(1)的推廣.證明的實質是確定集合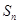 的個數及其表示形式.首先集合
的個數及其表示形式.首先集合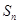 的個數最多有
的個數最多有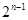 種情形,而每一種的值都不一樣,所以個數為
種情形,而每一種的值都不一樣,所以個數為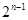 種情形,這是本題的難點,利用同一法證明. 確定集合
種情形,這是本題的難點,利用同一法證明. 確定集合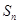 的表示形式,關鍵在于說明分子為奇數.由
的表示形式,關鍵在于說明分子為奇數.由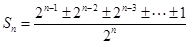 得分子必是奇數,奇數個數由范圍
得分子必是奇數,奇數個數由范圍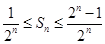 確定.
確定.
試題解析:解:(1)由已知, ,
,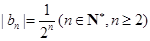 ,
,
∴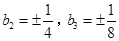 ,
,
由于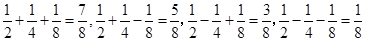 ,
,
∴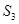 可能值為
可能值為 . 3分
. 3分
(2)∵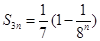 ,
,
當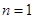 時,
時,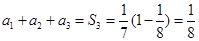 ,
,
當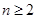 時,
時,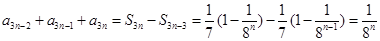 ,
,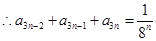 ,
, , 5分
, 5分
∵ 是
是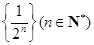 的生成數列,
的生成數列,
∴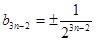 ;
;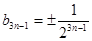 ;
;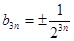 ;
;
∴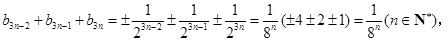
在以上各種組合中,
當且僅當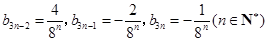 時,才成立.
時,才成立.
∴ . 8分
. 8分
(3)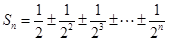 共有
共有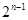 種情形.
種情形.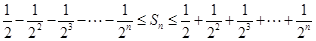 ,即
,即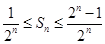 ,
,
又 ,分子必是奇數,
,分子必是奇數,
滿足條件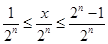 的奇數
的奇數 共有
共有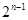 個. 10分
個. 10分
設數列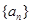 與數列
與數列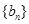 為兩個生成數列,數列
為兩個生成數列,數列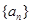 的前
的前 項和為
項和為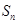 ,數列
,數列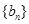 的前
的前 項和為
項和為 ,從第二項開始比較兩個數列,設第一個不相等的項為第
,從第二項開始比較兩個數列,設第一個不相等的項為第 項.
項.
由于 ,不妨設
,不妨設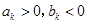 ,
,
則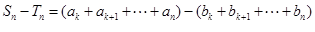
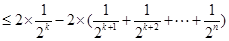
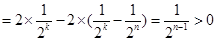


科目:高中數學 來源: 題型:解答題
已知數列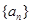 和
和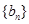 的通項公式分別為
的通項公式分別為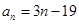 ,
,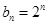 .將
.將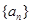 與
與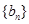 中的公共項按照從小到大的順序排列構成一個新數列記為
中的公共項按照從小到大的順序排列構成一個新數列記為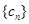 .
.
(1)試寫出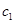 ,
,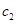 ,
,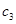 ,
,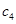 的值,并由此歸納數列
的值,并由此歸納數列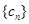 的通項公式;
的通項公式;
(2)證明你在(1)所猜想的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
若數列{an}滿足an+1=an+an+2(n∈N*),則稱數列{an}為“凸數列”.
(1)設數列{an}為“凸數列”,若a1=1,a2=-2,試寫出該數列的前6項,并求出前6項之和;
(2)在“凸數列”{an}中,求證:an+3=-an,n∈N*;
(3)設a1=a,a2=b,若數列{an}為“凸數列”,求數列前2011項和S2011.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
若無窮數列 滿足:①對任意
滿足:①對任意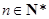 ,
,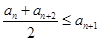 ;②存在常數
;②存在常數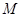 ,對任意
,對任意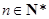 ,
,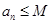 ,則稱數列
,則稱數列 為“
為“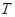 數列”.
數列”.
(Ⅰ)若數列 的通項為
的通項為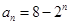
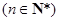 ,證明:數列
,證明:數列 為“
為“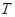 數列”;
數列”;
(Ⅱ)若數列 的各項均為正整數,且數列
的各項均為正整數,且數列 為“
為“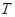 數列”,證明:對任意
數列”,證明:對任意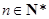 ,
,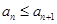 ;
;
(Ⅲ)若數列 的各項均為正整數,且數列
的各項均為正整數,且數列 為“
為“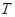 數列”,證明:存在
數列”,證明:存在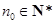 ,數列
,數列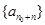 為等差數列.
為等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列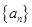 的通項公式為
的通項公式為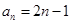 ,數列
,數列 的前
的前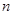 項和為
項和為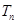 ,且滿足
,且滿足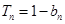 .
.
(1)求 的通項公式;
的通項公式;
(2)在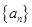 中是否存在使得
中是否存在使得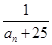 是
是 中的項,若存在,請寫出滿足題意的其中一項;若不存在,請說明理由.
中的項,若存在,請寫出滿足題意的其中一項;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com