
分析 (1)確定f(x)的定義域,求導數,確定f(x)在區間[$\frac{1}{e}$,e]上的最值只可能在f(1),f($\frac{1}{e}$),f(e)取到,即可求得結論;
(2)求導函數,分類討論,利用導數的正負,即可確定函數f(x)的單調性.
解答 解:(1)當a=-$\frac{1}{2}$時,f(x)=-$\frac{1}{2}$lnx+$\frac{1}{4}$x2+1,
∴f′(x)=$\frac{{x}^{2}-1}{2x}$,
∵f(x)的定義域為(0,+∞),
∴由f'(x)=0得x=1,
∴f(x)在區間[$\frac{1}{e}$,e]上的最值只可能在f(1),f($\frac{1}{e}$),f(e)取到,
而f(1)=$\frac{5}{4}$,f($\frac{1}{e}$)=$\frac{3}{2}$+$\frac{1}{{4e}^{2}}$,f(e)=$\frac{1}{2}$+$\frac{{e}^{2}}{4}$,
∴f(x)max=f(e)=$\frac{1}{2}$+$\frac{{e}^{2}}{4}$,f(x)min=f(1)=$\frac{5}{4}$.
(2)f′(x)=$\frac{(a+1{)x}^{2}+a}{x}$,x∈(0,+∞).
①當a+1≤0,即a≤-1時,f'(x)<0,
∴f(x)在(0,+∞)單調遞減;
②當a≥0時,f'(x)>0,∴f(x)在(0,+∞)單調遞增;
③當-1<a<0時,由f'(x)>0得x2>$\frac{-a}{a+1}$,
∴x>$\sqrt{\frac{-a}{a+1}}$或x<-$\sqrt{\frac{-a}{a+1}}$(舍去)
∴f(x)在($\sqrt{\frac{-a}{a+1}}$,+∞)單調遞增,在(0,$\sqrt{\frac{-a}{a+1}}$)上單調遞減;
綜上,當a≥0時,f(x)在(0,+∞)單調遞增;
當-1<a<0時,f(x)在($\sqrt{\frac{-a}{a+1}}$,+∞)單調遞增,在(0,$\sqrt{\frac{-a}{a+1}}$)上單調遞減;
當a≤-1時,f(x)在(0,+∞)單調遞減.
點評 本題考查導數知識的運用,考查函數的單調性與最值,考查分類討論的數學思想,正確分類是關鍵.


科目:高中數學 來源: 題型:解答題
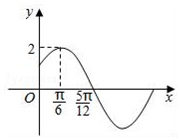 已知函數f(x)=Asin(ωx+φ)
已知函數f(x)=Asin(ωx+φ)查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,$\frac{9}{2}$] | B. | (-∞,1] | C. | (-∞,9] | D. | (-∞,8] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
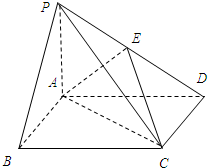 如圖,四棱錐P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E為PD的中點.
如圖,四棱錐P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{10}$ | B. | 10 | C. | $\frac{1}{5}$ | D. | 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com